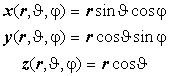Уравнение Шрёдингера для простейших стационарных движений

Во-вторых, можно смешать действительные орбитали разных уровней. Этот тип смешения называется гибридизацией. Обычно одна из них s-орбиталь (m=0). С ней можно смешать либо одну, либо две p-орбитали.

Каждая полученная гибридная функция обладает осью, вдоль которой ориентированы её пучности. Гибридные функции строятся так, чтобы их основные пучности были максимально удалены в пространстве друг

от друга. Гибрид из двух функций содержит две sp-орбитали. Их графики представлены на рис.

Из s-орбитали с двумя p-орбитали можно построить три равноценные линейные комбинации. Получается sp2-гибрид. Его пучности ориентированы под углами 120o.

Гибриды полезны для понимания механизмов образования химических связей.

6.3. Гамильтониан одномерного гармонического осциллятора:

В простейших случаях возвращающая сила (сила упругости) линейно зависит от смещения (закон Гука F=-kx), направлена против направления смещения, вызывая гармонические колебания массы относительно точки равновесия. Потенциальная энергия квадратично зависит от расстояния. Эта модель очень широко используется в квантовой механике.

Существует шутка, что блюда французской кухни приготовлены из минимума продуктов, но с огромным разнообразием соусов и приправ.

Параллельная шутка утверждает, что квантовая механика подобна французской кухне, но основным блюдом является гармонический осциллятор (или «вибратор» по В.А. Фоку) . Это преувеличение не слишком велико. Действительно, во времени движения в стационарных системах строго периодические, и их, как известно, всегда удаётся свести к набору простых гармонических движений.

Гамильтониан линейного гармонического колебания записывают в виде

.(6.7)

Квантование уровней колебательной энергии передаётся формулой:

.(6.8)

Волновые функции гармонического осциллятора графически напоминают волновые функции одномерного ящика, однако это лишь качественное сходство, а сами их характеристики устроены несколько иначе.

Основа их - гауссова функция Y0=A0×exp(-ax2). У неё нет узлов, и это вид волновой функции низшего, нулевого уровня.

У следующего, первого уровня должен быть один узел. Он возникает, если ввести функцию-сомножитель P1=x. При перемножении Y0 и P1 получается Y1= P1×Y0=A1×x×exp(-ax2).

У последующего, второго уровня должно быть два узла. Их можно получить, если полином-сомножитель это квадратичная парабола P2= (ax2+bx+c). Произведение P2×Y0 это функция вида Y2= A2× (ax2+bx+c)×exp(-ax2), но у неё остаётся лишь подобрать коэффициенты .

У третьего уровня должно быть три узла. Они возникают, если сомножитель организован в виде кубической параболы, и Y3= P3×Y 0= A2×(dx3+ex2+fx +g)×exp(-ax2).

Продолжая эту процедуру, нетрудно получить любую функцию спектра.

Численные коэффициенты в таком наборе функций подбираются из условия их нормировки и взаимной ортогональности, а именно:

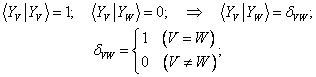
6.3.1. О характеристичности молекулярных колебаний.

Колебания различных химических связей обладают высокой степенью индивиду­альности. Это свойство называют характеристичностью. В колебательных спектрах частота и нередко даже графический вид колебательной полосы (или линии) поглощения какой-то определённой химической связи или группы (органического алкильного радикала или иного молекулярного фраг­мента) хо­рошо воспроизводятся в спектрах различных молекул, содержащих эти группы атомов. Эта индивидуальность является основой аналитического применения колебательной спектроскопии. Характеристики молекулярных колебаний можно получить с помощью различных методов спектроскопии инфракрасного (ИК) поглощения или спектроскопии комбинационного рассеяния (КР).

Диаграмма энергетических уровней и графики волновых функций осциллятора.

Уровни гармонического осциллятора согласно (6.8) эквидистанты, и соседние (Dv=1) отстоят на hn, где n собственная частота молекулярного колебания.

6.4. Качественное сравнение волновых функций одномерного ящика и осциллятора выявляет их качественное сходство. Число пучностей и узлов волновых функций увеличивается с но­мером уровня. Это свойство общее для всех квантовых систем.

6.5. Трёхмерный потенциальный «ящик». Модель одномерного «ящика» легко обобщается для трёхмерного движения в замкнутом пространстве параллелепипеда или куба. Рассмотрим для простоты куб с ребром L . Переменные независимы, и гамильтониан вида

.(6.9)

ведёт к аддитивной энергии и мультипликативным волновым функциям:

. (6.10)

(6.11)

6.6. Пространственное вращение. Общие свойства момента импульса.

При свободном вращении линейной молекулы относительно центра масс потенциальная энергия нулевая. Оператор кинетической энергии следует представить в шаровой системе координат.

6.6.1. Краткое содержание. Жёсткий ротатор и его уравнение Шрёдингера. Шаровые координаты (r, J, j). Элемент объёма. Лапласиан и уравнение Лапласа в ша­ровых координатах. Разделение переменных. Роль симметрии в выборе радиальной части общего решения. Радиальная и угловая части уравнения Шрёдингера и вид общего решения. Угловая часть уравнения Лапласа (уравнение Лежандра) и операторное уравнение для момента импульса. Квадрат модуля и проекция на ось вращения в шаровых переменных. Квантование модуля и квантование проекции момента импульса ротатора. Уровни энергии и их вырождение.

Радиальная переменная r

Угол широты J

Угол долготы j

Декартовы координаты:

Элемент объёма в шаровых переменных (см. рис.:

.(6.12)

Во многих задачах достаточно выделить элемент объёма, не зависящий от направления, и имеющий вид тонкого поверхностного слоя на шаре. В таком случае, избавляясь от угловых аргументов и оставляя лишь радиальную переменную, получаем сферический элемент объёма

 Скачать реферат