Расчет построения одноэтажных промышленных зданий

г) нагрузка от конструкций, сосредотачиваемая в узле подкрановой балки и колонны для торцевой рамы Мбт

Таблица 5

3.2 Редуцирование масс

Редуцирование масс – это приведение масс с уровня подкрановых балок на уровень покрытия в бескрановых рамах.

Матрица масс промежуточной рамы

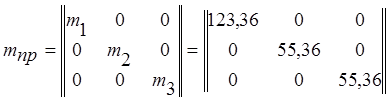(т)

Матрица масс торцевой рамы имеет вид

(т)

Отредуцированная масса на покрытии для промежуточной рамы:

mпр= Мпп+2*Мбп*0,2=123,36+2*55,36*0,2=145,504 (т)

Для торцевой рамы:

mтр= Мпт+2*Мбт*0,2=81,82+2*78,69*0,2=113,3(т)

3.3 Составление матрицы масс

Общий вид матрицы масс:

,

где ,

,

(т),

где Мкр+тел=66,5 т – маса крана с тележкой, Мгр=50 т – грузоподъемность крана;

(т)

(т*м2)

Итак, получили матрицу масс:

(т)

3. Расчет по пространственной расчетной схеме на динамическую нагрузку от крановой тележки.

При динамическом расчете одноэтажного промышленного здания с жестким в своей плоскости покрытием используется преобразованная расчетная схема, в которой ОПЗ путем приема редуцирования представляется в виде двухмассовой системы. Дискретные массы путем редуцирования приводятся в точку, расположенную в уровне покрытия и точку, расположенную в уровне тормозных конструкций. Ткр

Крановую нагрузку при торможении тележки рассматривают по графику (рис. 10).

Нагрузка носит почти ударный характер.

При торможении возникают колебания

0,02 1,99 2,0 t ,c

Дифференциальное уравнение, описывающее колебания ОПЗ под действием динамической нагрузки:

||M||×{q(t)} + ||X||×{q(t)} + ||C||×{q(t)} = {P(t)}(1), где

||M|| - матрица инерционных параметров здания;

||X|| = 2x||M|| - матрица коэффициентов сопротивления, где

x - коэффициент демпфирования, определяемый по формуле:

x = dwn / 2pÖ1+(d/2p)

(d - логарифмический декремент затухания, равный для стальных конструкций 0,3, wn - собственная частота колебаний по n-той форме)

||C|| - матрица жесткости здания;

{q(t)} – вектор смещения расчетных точек;

{P(t)} – вектор динамической крановой нагрузки.

Для решения уравнения (1) используется метод разложения по главным формам колебаний, согласно которому смещение расчетных точек представляется в виде суммарных амплитудных значений смещений по главным формам колебания.

Смещение представлено интегралом Дюамеля:

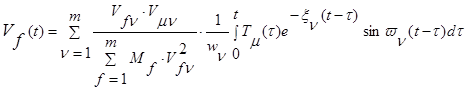, где

f – номер расчетной точки;

n - номер формы колебания;

Vfn, Vmn - амплитудные значения смещений расчетных точек f и m при n-то форме колебания;

m - расчетная точка, где приложена динамическая крановая нагрузка;

Mf - масса расчетной точки f;

vn - собственная частота колебания с учетом затухания:

vn = Öwn2 + nn2

t - текущая функция t;

Rm(t) - значение нагрузки от торможения крановой тележки в расчетной точке m в момент времени t;

Rm - крановая нагрузка, приложенная в расчетной точке m.

При пространственной расчетной схеме расчетная крановая нагрузка определяется следующим образом:

- нормативная нагрузка, возникающая от торможения крановой тележки на 1-ом колесе

Рmaxn = f × (Gт + Q×g) / n0, где

f – коэффициент трения, зависящий от типа подвеса груза;

Gт – вес тележки, кН;

Q – грузоподъемность крана, т;

g = 9,8 Н/кг – ускорение свободного падения;

n0 – число колес с одной стороны мостового крана.

крановая нагрузка от торможения тележки, действующая на колонну

Tmax = Tmaxn × n × gн × ns × Sу, где

n=1,1 – коэффициент перегрузки;

 Скачать реферат