Операторный метод анализа переходных колебаний

Операторное напряжение на емкости равно произведению операторного емкостного сопротивления на величину операторного тока.

Выражения

представляют закон Ома в операторной форме.

Выводы:

– законы Кирхгофа и Ома справедливы и в операторной форме, причем закон Ома справедлив только при нулевых начальных условиях;

– все ранее изученные методы анализа электрических цепей (метод контурных токов, метод узловых напряжений, метод эквивалентного генератора и др.) справедливы и в операторной форме;

3. Операторные схемы замещения реактивных элементов при ненулевых начальных условиях

Часто коммутация осуществляется в момент времени, когда реактивные элементы обладают энергией. В этом случае они находятся при ненулевых начальных условиях и к ним нельзя применить закон Ома в операторной форме. Для устранения этого препятствия используют прием, суть которого состоит в том, что физически один реактивный элемент искусственно заменяют двумя: операторным источником, отражающим энергию реактивного элемента на момент коммутации, и самим реактивным элементом, но находящимся теперь уже при нулевых начальных условиях. Такое изображение называется схемой замещения. Ее можно получить, используя свойства преобразования Лапласа:

.

Так, для индуктивности с током схемы замещения имеют вид, показанный на рисунке 1.

а) б) в)

Рис. 1

Они являются следствием преобразования следующих выражений:

;

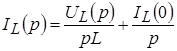
Здесь следует иметь в виду два обстоятельства: направление операторного тока должно совпадать с направлением тока через индуктивность в момент непосредственно предшествующий коммутации и второе, что реально существует один элемент, поэтому операторный ток через индуктивность в схеме замещения определяется в общей ветви (рис. 1б).

Заряженная емкость отображается схемами замещения, показанными на рисунке 2б, в.

а) б) в)

Рис. 2

Они являются следствием преобразования следующих выражений:

,

.

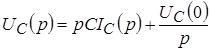Здесь напряжение операторного источника совпадает с напряжением на емкости до коммутации, а операторное напряжение на емкости определяется между зажимами 1 – 1¢.

Применение операторных схем замещения реактивных элементов, находящихся при ненулевых начальных условиях, дает возможность применять закон Ома в операторной форме, что широко используется на практике и, в частности, при рассмотрении свободных колебаний в электрических цепях. Известно, что такие колебания возникают за счет энергии, запасенной реактивными элементами при отключении внешних источников. Следует иметь в виду, что указанная коммутация может осуществляться как путем механического отключения, так и путем гашения источников. В последнем случае источник напряжения заменяется коротким замыканием, а источник тока – обрывом.

При решении задач приходится осуществлять переход от обычной к операторной схеме. Если реактивные элементы находятся при ННУ, то такой переход не вызывает особых затруднений. Например, на рисунке 3, а показана исходная схема, а на рисунке 3, б – эквивалентная ей операторная.

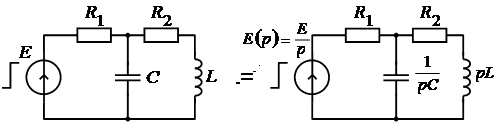
а) б)

Рис. 3

Если же реактивные элементы находятся при ненулевых начальных условиях, то в операторной схеме они должны быть отображены схемами замещения.

Пример.

Пусть в цепи, изображенной на рисунке 4 в момент замыкается ключ "К". Требуется определить эквивалентную ей операторную схему.

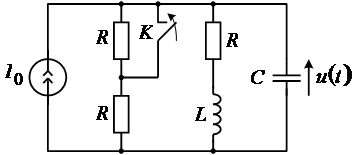
Рис. 4

Так как реактивные элементы в данном случае находятся при ненулевых начальных условиях, то предварительно следует определить и . Для этого изобразим эквивалентную схему цепи при (рис. 5).

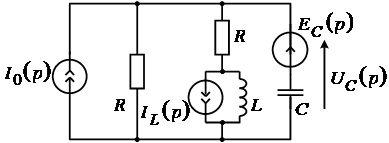
Рис. 5

Видно, что ; .

Таким образом ; и соответствующая этому схема показана на рисунке 6.

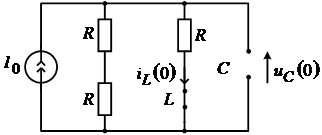
Рис. 6

Далее находится требуемая реакция в операторной форме, а затем осуществляется переход в область реального времени.

Вывод: нахождение реакций при ненулевых начальных условиях требует применения схем замещения в операторной форме и является более сложной задачей, чем при ННУ.

Библиографический список

1. Белецкий А.Ф. ТЛЭЦ: учебник для вузов. – М.: Радио и связь, 1986. С. 218 – 226.

2. Шалашов Г.В. Переходные процессы в электрических цепях. –с. 7 – 20.

3. Бакалов В.П. ТЭЦ: учебник для вузов. – М.: Радио и связь, 1998 г. с. 169 – 180.

 Скачать реферат