Анализ структуры цен на фондовом рынке

Поясним сущность регрессии с переключениями на примере. С этой целью рассмотрим рисунок 4.

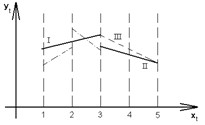
Рисунок 4 – Пример регрессии с переключениями

На данном рисунке приведен скачкообразный переход от регрессии I к регрессии II. Непрерывный переход от регрессии I к регрессии III, изображенных пунктирной линией также приведен н

а рисунке 4.

На рисунке 4 штрихпунктирной линией показано изменение коэффициента регрессии на каждом шаге (адаптивный алгоритм) [13].

Использование априорной информации позволяет повысит точность оценивания параметров регрессии. Это важно при построении математических моделей экономических процессов, так как часто исходными данными являются короткие временные ряды. Предположим что область параметров задается в виде нечетких ограничений – равенств и неравенств. Рассматриваемая регрессия имеет вид

(17)

где - зависимая переменная, - параметр регрессии, – независимая переменная, - случайная величина, здесь и далее « / » означает транспонирование. Относительно регрессоров далее используется такое допущение

Допущение 1. Матрица невырождена

Лемма 1. Если выполняется допущение 1 и (- выпуклое множество), то строго монотонно возрастает, а строго монотонно убывает при , где

Рассматриваемую задачу можно трактовать как задачу с двумя нечеткими целями выбора, так как с ростом r увеличивается первый критерий и уменьшается второй, и наоборот. Нечеткой i - целью, i = 1,2 , в множестве Z является некоторое его нечеткое подмножество, обозначим его . Функция принадлежности

(18)

где .

Согласно лемме 1, уменьшается от 1 до 0, а увеличивается от 0 до 1.

Рассмотрим модель регрессии с переключением при одномерном переключателе, зависящем от времени t:

, (19)

где - n – мерный вектор регрессоров, - n – мерный вектор истинных значений параметров регрессии, - индекс точки переключения, - шум.

На отрезке времени с числом наблюдений параметры регрессии постоянны и равны . Пусть . Далее будем считать, что точки переключения известны, а величина может быть меньше n.

Пусть параметры регрессии на соседних отрезках It и It +1 достаточно близки, что можно сформулировать в виде нечеткого ограничения-равенства , где – вектор, его компоненты – нечетко заданные числа, функции принадлежности которых сосредоточены в окрестности 0.

Расхождения, аналогичные приведенные в разделе 1, показывают, что задачу оценивания можно сформулировать как двухкритериальную.

(20)

(21)

где, , - выпуклое множество, и - весовые коэффициенты (известные величины). В частности,

Введем следующие матрицы:

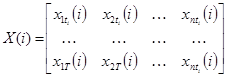
размерности mi x n;

X = diag (X(1), …, X(N)) размерности

;

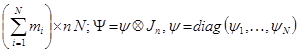Сформируем матрицу

.

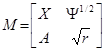Здесь r > 0 , ,

где матрица 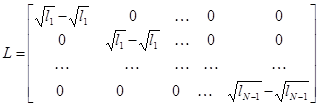имеет размерность

(N-1)xN.

Имеем

где - вектор, размерность которого .

Причем .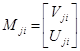

Здесь

где , .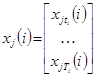

Размерность равна . У вектора размерности компонента с индексом равна , с индексом - равна , остальные компоненты нулевые.

Относительно регрессоров принимаем допущение

Допущение 6. У матрицы 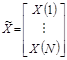размерности столбцы линейно независимы.

 Скачать реферат