Вопросы устойчивости и общие сведения об автогенераторах

Пример 8.2.

Пусть дана электрическая цепь второго порядка с характеристическим уравнением

Пользуясь критерием Михайлова оценить устойчивость.

Решение задачи.

Заменим р на jw и получим

Вычислим вещественную и мнимую части N (jw) для неско

льких значений w и сведем полученные результаты в таблицу 8.1.

Таблица 8.1.

Изобразим годограф N (jw) на комплексной плоскости (рис. 8.2).

Очевидно, что с ростом частоты w конец вектора N (jw) последовательно проходит два квадранта, начиная с первого. Следовательно, согласно критерию Михайлова, цепь устойчива.

Рис. 8.2. Построение годографа полинома знаменателя

Пример 8.3.

Пусть электрическая цепь описывается передаточной функцией

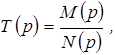
где

Оценить устойчивость электрической цепи.

Решение задачи.

Заменим р на jw и получим

Используя критерий Михайлова, построим годограф функции N (jw), давая последовательно значения частоты w от 0 до ¥ (рис. 8.3):

Рис. 8.3. Годограф функции N (jw)

Очевидно, что в данном случае электрическая цепь не является устойчивой, так как конец вектора из первого квадранта переходит в четвертый и затем в третий, т. е. нарушается последовательность обхода, хотя общее число квадрантов, в которых побывал конец вектора, равно трем, т. е. совпадает с порядком характеристического уравнения N (р).

Критерий Найквиста. Этот критерий, как и критерий Михайлова, является частотным (в отличие от алгебраического критерия Гурвица). Он позволяет судить об устойчивости усилителя с обратной связью по виду частотной характеристики данного усилителя при разомкнутой цепи ОС. Суть критерия состоит в следующем. Система с ОС устойчива, если годограф разомкнутой системы не охватывает точку на комплексной плоскости с координатами (1, j0). В противном случае система будет неустойчива и может рассматриваться как автогенератор.

Рассмотрим критерий подробнее. На рисунке 8.4 показана схема усилителя с ОС.

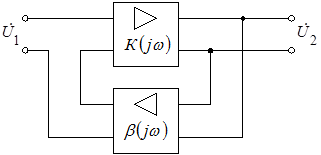
Рис. 8.4. Схема усилителя с ОС

Можно записать

.

Тогда частотная передаточная функция этой системы будет равна

Отсюда

(8.4)

Система (рис. 8.4) будет неустойчивой, если знаменатель передаточной функции (8.4) обратится в нуль:

Очевидно, что это возможно при выполнении двух условий:

1) (8.5)

2) (8.6)

Условия (8.5) и (8.6) называют, соответственно, условиями баланса амплитуд и баланса фаз. Физически они означают, что для самопроизвольного нарастания амплитуды собственных колебаний (возникающих, например, в виде незначительных флуктуаций теплового тока активного элемента) необходимо, чтобы колебания, возвращаемые на вход усилителя по цепи ОС, совпадали по фазе с существующими во входной цепи (баланс фаз), при этом общее усиление должно быть достаточным для компенсации потерь в пассивных цепях (баланс амплитуд).

Если систему, приведенную на рисунке 8.4, представить в разомкнутом виде (рис. 8.5), то общий коэффициент усиления можно записать в виде:

(8.7)

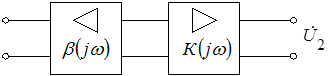
Рис. 8.5. Схема усилителя с разомкнутой цепью ОС

Изменяя значение частоты w от 0 до ¥ и откладывая полученные значения модуля и фазы на комплексной плоскости, получим годограф вектора передаточной функции. Точка с координатами (1, j0) соответствует значениям фазы (k = 0, 1, 2, …) и модуля а это и есть рассмотренные условия самовозбуждения.

Таким образом, если годограф передаточной функции охватывает точку с координатами (1, j0), то система (рис. 8.5) будет неустойчивой при замкнутой цепи ОС, так как будет хотя бы одна частота wГ, на которой будут выполняться условия баланса амплитуд и фаз, и усилитель самовозбудится.

На рисунке 8.6 показаны годографы устойчивой (а) и неустойчивой (б) систем соответственно.

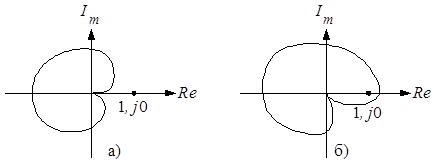
Рис. 8.6. Годографы устойчивой (а) и неустойчивой (б) систем

Возможен случай, когда система устойчива, но для нее справедливы соотношения (8.5) и (8.6). Ей соответствует годограф, представленный на рисунке 8.7. На практике такие системы встречаются редко и не представляют практического интереса в теории автоколебательных цепей.

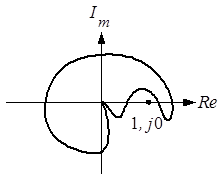
Рис. 8.7. Пример годографа устойчивой системы, для которой выполняются условия самовозбуждения

Рассмотрим несколько примеров на определение устойчивости электрических цепей.

Пример 8.4.

Исследовать устойчивость усилителя с резистивно-емкостной нагрузкой, выход которого непосредственно соединен с входом (рис. 8.8).

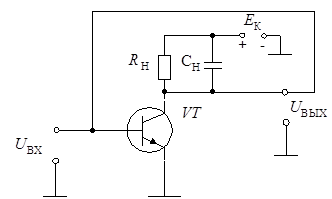
Рис. 8.8. Схема усилителя с резистивно-емкостной нагрузкой

 Скачать реферат