Исследование уровня креативности менеджеров по рекламе

Таким образом, с учетом статистических значе

ний индекса дискриминации (+1 до -1), мы удаляем из теста задания под номерами 14, 15, 24, 27, 28, 29, 46, 47, так как в случаях, когда значение индекса дискриминации приближается к нулю или отрицателен, проверяемый пункт теста должен быть пересмотрен в связи с некорректностью формулировки задания или вариантов ответа на него.

4. Определение надежности теста

4.1 Определение надежности целого теста

Термином «надежность» характеризуется воспроизводимость, или стабильность, результатов тестирования. Если распределение тестовых оценок какой-либо группы, прошедшей тестирование когнитивных способностей, имеет простую среднюю арифметическую, равную 100, а через неделю у той же группы эта мера средней тенденции окажется равной 72, мы вынуждены будем заподозрить что-то неладное. Мы сочтем этот тест ненадежным, потому что его результаты не воспроизводятся. Общеизвестно, что результаты повторного тестирования одной и той же группы людей всегда несколько отличаются от результатов их первого тестирования, но если эта разница существенна, значит либо в самом тесте, либо в методике обсчета его результатов есть какой-то изъян.

Известны три метода определения надежности теста: метод определения ретестовой надежности, метод определения надежности взаимозаменяемых форм теста и метод определения надежности расщеплением. Метод определения ретестовой надежности основан на двукратном тестировании одной и той же группы людей и корреляции двух распределений тестовых оценок. Чем меньше коэффициент корреляции, называемый в данном случае коэффициентом надежности, отличается от +1 — идеального значения для положительной корреляции, — тем более надежным считается тест. В идеале, коэффициент надежности теста, который предполагается использовать в отборочном процессе, должен быть более +0,8, однако на практике приемлемым считается и тест с коэффициентом надежности, равным примерно +0,7. Однако этот метод имеет несколько ограничений. Экономически невыгодно дважды отвлекать людей от работы только для того, чтобы протестировать их. Кроме того, может сказаться и эффект научения: во-первых, люди запоминают вопросы после первого тестирования, а во-вторых, в промежутке между двумя тестированиями они могут приобрести определенный дополнительный опыт, в результате чего тестовые оценки во второй раз будут выше.

Метод определения надежности взаимозаменяемых форм теста тоже базируется на двукратном тестировании, однако в данном случае для повторного тестирования используется не тот же самый тест, а его эквивалентная, или параллельная, форма. Недостатком этого метода является то, что разработка двух самостоятельных и эквивалентных тестов непростая и дорогостоящая процедура.

Метод определения надежности расщеплением заключается в том, что после однократного применения теста входящие в него вопросы делят пополам с последующей корреляцией тестовых оценок за каждую из них. Преимущество этого метода в том, что он не требует больших затрат времени и позволяет ограничиться одним тестированием. При этом исключаются факторы, способные повлиять на вторую оценку.

В нашем исследовании повторное тестирование производилось спустя 36 дней с максимально приближенными условия первого тестирования.

Таблица 4.

Распределение индивидуальных баллов испытуемых по ретесту

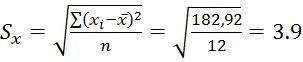
- коэффициент корреляции Пирсона

Наименьшее значение ретестовой надежности целого теста равно 0,7. Таким образом, наше значение позволяет сделать вывод, что наш тест надежен.

4.2 Определение надежности частей теста

Надежность частей теста – характеристика надежности психодиагностической методики, получаемая путем анализа устойчивости результатов отдельных совокупностей тестовых задач или единичных пунктов теста. Наиболее распространенным способом определения надежности частей теста является метод расщепления, суть которого заключается в выполнении испытуемым заданий двух равноценных частей теста.

Для того, чтобы вычислить надежность частей теста необходимо сначала вычислить стандартное отклонение половины теста.

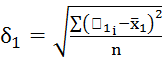
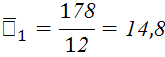
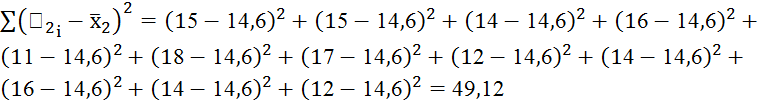
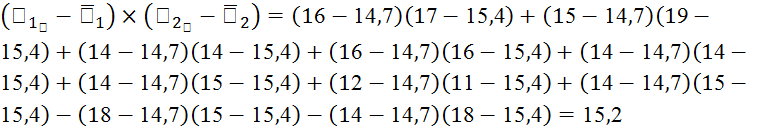
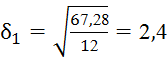
Далее вычисляем коэффициент надежности половины теста по следующей формуле:

 Скачать реферат