Численное интегрирование функций

. (6)

Рис. 3.

Формула Симпсона. Разобьем интервал интегрирования на 2n равных частей длиной width=112 height=25 src="images/referats/3078/image030.png">. На каждом отрезке [xi, xi+2] подынтегральную функцию f(х) заменим параболой, проходящей через точки (xi, yi), (xi+1, yi+1), (xi+2, yi+2). Тогда приближенное значение интеграла определяется формулой Симпсона:

. (7)

При вычислениях на ЭВМ более удобна следующая формула:

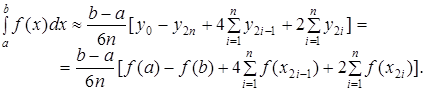
Метод Симпсона - один из наиболее широко известных и применяемых методов численного интегрирования, он дает точные значения интеграла при интегрировании многочленов до третьего порядка включительно.

Формула Ньютона. Приближенное значение интеграла по формуле Ньютона вычисляется следующим образом:

где число участков разбиения кратно трем, т.е. составляет 3n. При разработке программ для ЭВМ удобнее использовать эквивалентную формулу:

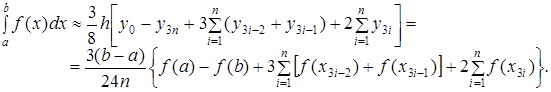
Метод Ньютона дает точные значения интеграла при интегрировании многочленов до четвертого порядка включительно.

3. Автоматический выбор шага интегрирования

В результате расчета по формулам (3) - (8) получают приближенное значение интеграла, которое может отличаться от точного на некоторую величину, называемую погрешностью интегрирования. Ошибка определяется формулой остаточного члена R, различной для каждого из методов интегрирования. Если требуется вычислить значение интеграла с погрешностью, не превышающей e, то необходимо выбрать такой шаг интегрирования h, чтобы выполнялось неравенство R(h) £ e. На практике используют автоматический выбор значения h, обеспечивающего достижение заданной погрешности. Сначала вычисляют значение интеграла I(n), разбивая интервал интегрирования на п участков, затем число участков удваивают и вычисляют интеграл I(2n). Процесс вычислений продолжают до тех пор, пока не станет справедливым условие:

,

где P – порядок точности квадратурной формулы. Для формул левых и правых прямоугольников P = 1, для формул центральных прямоугольников и трапеций P = 2, для формул Симпсона и Ньютона P = 4. В результате полагают, что I » I(2n) с точностью e.

Заключение

В ходе выполнения курсовой работы был проведен сравнительный анализ численных методов, таких как численное интегрирование.

В настоящее время появилось значительное число различных программных продуктов (MathCAD, MathLAB и т.д.), с помощью которых, задавая только входные данные, можно решить значительное число задач.

Для более глубокого анализа численных методов мы использовали средства MathCAD, а также алгоритмические языки программирования.

Библиографический список

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Гос. изд-во физ.-мат. литературы, 1960. 659 с.

2. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высш. шк., 1994. 544 с.

3. Ракитин В.И., Первушин В.Е. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров: Учеб. пособие. М.: Высш. шк., 1998. 383 с.

4. Калиткин Н.Н. Численные методы. М.: Наука, 1978.

Размещено на http://www.allbest.ru

 Скачать реферат