Разбиение натурального ряда

[(1+)n/2]

=[(1+)n/2]+n=[(3+)

n/2]

Выведем из явных формул гипотезу Акулича.

Обозначим

;

Рассмотрим натуральное число N и выясним сколько a-чисел и b-чисел среди первых N натуральных чисел, если последовательности заданы формулами:

;

Неравенства равносильно, по определению целой части, неравенству <N+1, т.е. неравенству n<(N+1)/. Значит, a-чисел среди первых N натуральных чисел имеется ровно [(N+1)/]. Аналогично, b-чисел

[(N+1)/]

Тогда отношение количества a - чисел к количеству b- чисел равно

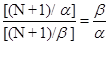
Устремим N к бесконечности, получим

Гипотеза оказалась верна, при условии что обе последовательности и заданы явными формулами

[(1+)n/2]

=[(3+)n/2]

Но Акулич не первый догадался представить последовательности и в виде [] и [].

Эти же явные формулы получаются из формул Рэлея при x = 2/(1+), поскольку при этом величина 1-x равна как раз 2/(3+), т.е.

Возникает вопрос об единственности разбиения множества N на две последовательности.

В статье Баабабова [2] доказывается теорема, обобщающая этот результат и утверждает, что таких разбиений натурального ряда существует бесконечно много. Приведем данную теорему и ее подробное доказательство.

Обозначим

Теорема.

Если и - положительные иррациональные числа, связанные соотношением , то среди чисел вида [] и [] , где n , каждое натуральное число встречается ровно один раз.

Доказательство:

Поскольку > 1, в последовательности никакое число не повторяется. Аналогично вследствие неравенства >1 строго возрастает и последовательность

Действительно, пусть [] – k

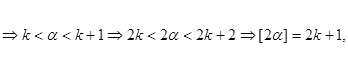
Следовательно,

Докажем теперь, что каждое натуральное число встречается ровно один раз.

Предположим, что некоторое натуральное число k вошло в обе последовательности т е k = , где m,n – натуральные числа. Тогда должны быть выполнены неравенства

k<< k + 1, k<<k + 1,

т.е.

сложим эти неравенства, не забывая про условие

Получим

откуда k<m+n<k+1

Но такого для натуральных чисел не может быть. Значит, число k не могло войти в обе последовательности.

Теперь предположим, что k не вошло ни в одну из последовательностей. Тогда для некоторых натуральных чисел m и n должны выполняться неравенства

m < k <k+1< (m+1)

n < k <k+1< (n+1)

которые можно преобразовать к виду

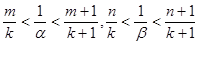
складывая, получаем

откуда m+n<k и k+1<m+n+2 m+n<k и m+n>k-1

Такого для натуральных чисел тоже не может быть. Получаем противоречие, следовательно, теорема доказана.

В следующем параграфе рассмотрены упражнения о разбиениях натурального ряда, при решении которых используются результаты данного параграфа.

§3. Упражнения

 Скачать реферат