Линейные электрические цепи постоянного и синусоидального тока

Задание 1

Принципиальная схема цепи выглядит следующим образом:

Найдем количество уравнений. Так как в цепи присутствуют независимые источники тока, то мы имеем:

Теперь выберем независимые контуры. Пусть первый контур состоит из ветвей 1, 4, 5, и по нему течет ток I11 по часовой стрелке. Пусть второй контур состоит из ветвей 2, 4, 6, по нему течет ток I22 по часовой стрелке.

Запишем систему уравнений по методу контурных токов:

(R3+R4)*I11-R4*I22=-E6

(R1+R7+R4+R5)*I22-I11*R4 – J1*R5=E5

15 * I11 – 5 * I22 = -5,

-5 * I11 + 15 * I22 = 15;

Решим систему по методу Крамера. Найдем определители:

D = 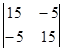= 200, D22 = 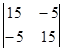= 200, D11 = 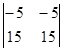= 0.

Найдем контурные токи:

I11 = D11/D = 0 A; I22 = D22/D = 1 A

Теперь посчитаем токи во всех ветвях.

Через хорды текут только контурные токи, поэтому:

I3 = I22 = 0 A

I1 = I11 = 1 A

В ветви с источником тока течет ток, создаваемый этим источником:

I2 = J1 = 1A

Токи в остальных ветвях найдем как сумму контурных токов, текущих по ним, с учетом знаков:

I4 = I22 – I11 = 1 A

I6 = J1-I11 = -1 A

I5 = I22 + J1 = 2 A

Проверка

1) Балланс мощностей:

E5*I5 + E6*I6 +J2*(U2+I2*R2) = I1^2*R1+I2^2*R2+I3^2*R3+I4^2*R4+I5^2*R5+I1^2*R7

40 Вт = 40 Вт.

2) Проверка по первому закону Киргофа:

I1 = I5 + I3;

I1 = I2 + I4;

I4 = I5 + I6;

I2 + I6 = I3;

Задание 2

Принципиальная схема цепи выглядит следующим образом:

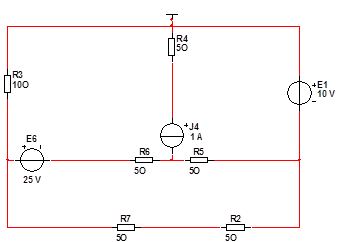
Найдем количество уравнений. Так как в цепи присутствуют независимые источники тока, то мы имеем:

Теперь выберем независимые контуры. Пусть первый контур состоит из ветвей 1 и 2, и по нему течет ток I11 против часовой стрелки. Пусть второй контур состоит из ветвей 1 и 3, по нему течет ток I22 против часовой стрелки.

Запишем систему уравнений по методу контурных токов, учитывая J1:

(R3 + R6 +R5) * I11 – (R5 + R6) * I22 = – (R3 + R6) * J1 – E6 + E1

– (R5 + R6) * I11 + (R2 + R5 + R6 + R7) * I22 = R6 * J1 + E6

20 * I11 – 10 * I22 = -30

-10 * I11 + 20 * I22 = 30

Решим систему по методу Крамера. Найдем определители:

D = 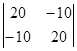= 300, D11 = = -300, D22 = = 300.

Найдем контурные токи:

I11 = D11/D = -1 A; I22 = D22/D = 1 A

Токи в ветвях найдем как сумму контурных токов, текущих по ним, с учетом знаков:

I2 = I7 = I22 = 1A

I6 = – I11 + I22 – J1 = 1A

I5 = I11 – I22 = -2 A

I4 = J1 = 1A

I3 = I11 + J1 = 0

I1 = I11 = -1A

Проверка

1) Балланс мощностей:

I3*I3*R3 + I4*I4*R4 + I5*I5*R5 + I6*I6*R6 + I2*I2*(R2+R7) = E6*I6 + E1*I1 + J4 * U4,

5 + 5 + 20 + 10 = 25 – 10 + 25,

40 = 40

2) Проверка по первому закону Киргофа:

I4 + I1 = I3;

I6 + I3 = I2;

I4 + I5 + I6 = 0;

I1 = I2 + I5;

Задание 3

Принципиальная схема цепи выглядит следующим образом:

Преобразуем данную схему. Ветвь 1 исключим. Позже ток в этих ветвях найдем через закон Киргофа. Далее, найдем сопротивление, эквивалентное сопротивлению между узлами 1 и 2 (участок схемы с ветвями 1, 5, 7, 8).

Rэ = 1/(1/R5 + 1/R4) = 8/3 (Ом)

И заменим этот участок на одну ветвь с сопротивлением, равным Rэ. Получим следующую схему:

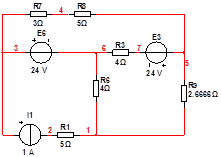
Найдем количество уравнений. Так как в цепи присутствуют независимые источники тока, то мы имеем:

Начертим граф. Пусть ветвь 1 составляет дерево.

			2

I22

Теперь выберем независимые контуры. Пусть первый контур состоит из ветвей 1, 4, 5, и по нему течет ток I11 по часовой стрелке. Пусть второй контур состоит из ветвей 2, 4, 6, по нему течет ток I22 по часовой стрелке.

Запишем систему уравнений по методу контурных токов:

I11*(R7+R3) – I22*R3 = E6 – E3

– I11*R3 + I22*(R2 + R3 + R4) = E3 + J1*R2

12*I11 – 4*I22=0,

32/3*I22 – 4*I11= 28;

Решим систему по методу Крамера. Найдем определители:

D = 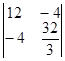= 112, D22 = = 336, D11 = 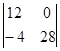= 112.

 Скачать реферат