389 Единое электродинамическое поле

Таким образом, имеем очевидное обобщение и серьезное развитие представлений классической электродинамики. В частности, показано, что в Природе, так же как и в случае ЭМ поля, не может быть электрического, магнитного или другой составляющей единого электродинамическогополя с одной полевой компонентой. Структура обсуждаемых составляющих единого электродинамического поля из двух векторных взаимно

ортогональных полевых компонент – это объективно необходимый способ их реального существования, принципиальная и единственная возможность распространения конкретной составляющей в виде потока соответствующей физической величины, в случае динамических полей – посредством поперечных волн.

Форма представленных систем уравнений (1) – (4) говорит о существовании волновых уравнений как для компонент ЭМ поля и , так и для компонент поля ЭМ векторного потенциала и . В этом можно убедиться, взяв, как обычно, ротор от одного из роторных уравнений любой системы, и после чего подставить в него другое роторное уравнение той же системы. В качестве иллюстрации получим, например, для системы (2) волновое уравнение относительно :

.

Здесь, согласно (2c), , - оператор Лапласа, а - фазовая скорость поля волны в отсутствие поглощения. Следовательно, указанные волновые уравнения описывают волны конкретной составляющей единого электродинамического поля в виде одной из парных комбинаций этих четырех волновых уравнений. В итоге возникает физически очевидный вопрос, что это за волны, и каковы характеристики распространения таких волн?

Ввиду того, что уравнения систем (1) и (2) математически структурно тождественны, а волновые решения уравнений (1) широко известны [6], то далее анализ характеристик распространения составляющих единого электродинамическогополя, например, в виде плоских волн в однородных изотропных материальных средах проведем, прежде всего, для уравнений (3) электрического поля и уравнений (4) магнитного поля. Их необычные структуры между собой также математически тождественны, а волновые решения систем этих уравнений, как будет показано ниже, физически весьма нетривиальны.

Итак, рассмотрим волновой пакет плоской линейно поляризованной электрической волны, распространяющейся вдоль оси 0X с компонентами и для системы (3) либо магнитной волны с компонентами и для системы (4), которые представим комплексными спектральными интегралами. Здесь, согласно соотношениям (5с) и (5d), учтена функциональная взаимосвязь обсуждаемых волн в виде единого процесса и взаимная коллинеарность векторов и (эти векторы антипараллельны), и компонент полей. Тогда, например, для уравнений электрического поля указанные интегралы имеют вид:

и ,

где и - комплексные амплитуды.

Подставляя их в уравнения (3a) и (3c), приходим к соотношениям и . Соответствующая подстановка интегралов и в уравнения (4а) и (4c) дает и . В итоге для обеих систем получаем общее для них выражение:

В конкретном случае среды идеального диэлектрика () с учетом формулы из следует для обеих систем обычное дисперсионное соотношение [6], описывающее однородные плоские волны электрического или магнитного полей. При этом связь комплексных амплитуд компонент указанных волновых полей имеет специфический вид:

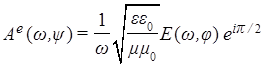в системе (3) и

в системе (4),

то есть при распространении в диэлектрической среде компоненты поля сдвинуты между собой по фазе на π/2. Специфика здесь в том, что характер поведения компонент поля такой волны в любой точке пространства аналогичен кинематическим параметрам движения (смещение и скорость) классической частицы в точке устойчивого равновесия поля потенциальных сил. Конечно, математически данный результат очевидно тривиален, поскольку компоненты ЭМ поля и поля ЭМ векторного потенциала связаны между собой посредством производной по времени (см. соотношения (5c) и (5d)). Однако с физической точки зрения этот результат весьма нетривиален и, безусловно, интересен и наводит на размышления.

Для проводящей среды () в асимптотике металлов () дисперсионное соотношение систем уравнений (3) и (4) имеет обычный в таком случае вид , где [6]. Тогда, например, для уравнений (3) связь комплексных амплитуд компонент иметь вид и волновые решения запишутся в виде экспоненциально затухающих в пространстве плоских волн со сдвигом начальной фазы между компонентами поля на π/4:

, (10)

.

 Скачать реферат