Философия науки

Пусть электрон проходит через одноатомную пленку, как показано на рис.4.

Когда электрон движется в области электромагнитных взаимодейст­вий, мы должны рассматривать его как частицу. Вероятность обнаружить его в точке A(xo, yo, zo, to) 4-пространства всегда равна 1. Уравнение Шре­дингера, как известно, не способно предсказать этот результат.

Пусть теперь электрон движется в области квант

овых и электромаг­нитных взаимодействий, т.е. между атомами. Благодаря взаимодействию свойства электрона (масса, структура и т.д.) будут напоминать свойства волны. Схема, изображенная на рис.4, есть только иллюстрация. Если мы придерживаемся научной логики, мы не должны эклектически объединять в единый узел взаимоисключающие свойства. Всегда необходимо определять границы применимости понятий, т.е. условия, при которых возникают и исчезают те или

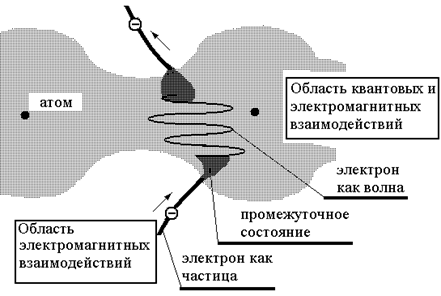
Рис. 4

иные свойства[1]. Возможно, такой подход позволил бы ос­во­бодиться от вероятностной интерпретации функциии перейти от кван­товой ме­ханики точечных частиц к механике протяженных частиц. Эта идея имеет право на су­ществование и проверку.

1.4 Общие категории.

Рассматривая частно-научные категории, мы показали, что в них вхо­дят как обя­зательная часть философские категории. Теперь мы рассмотрим некоторые категории, которые являются общими для физики и философии. Это: материя, про­странство, время, взаимодействие, состояние и другие. Благодаря Общей теории относительности наиболее интересными для анализа являются про­странство и время. Проблема пространства и времени обширна. Здесь мы рассмотрим только те во­просы, которые либо ускользают из внимания исследователей, либо излагаются с ошибками.

Пространство. Главные проблемы этой категории – кривизна про­странства и взаимосвязь пространства и эфира. Чтобы установить нали­чие кривизны пространст­ва, используют следующий прием. В пространстве выбираются две точки a и b (см. рис.5). В точке a выбирается некоторый вектор Aa и перемещается в точку b. Обозна­чим перенесенный вектор в этой точке как Ab . Теперь мы имеем два вектора, которые мы можем срав­нить. Если Aa ≠ Ab , то можно утверждать, что пространство криволи­нейно.

Это “простое” доказательство имеет существенный изъян. Мы не мо­жем срав­нить вектора непосредственно. Для этого один из векторов мы должны перенести в точку, где находится первый вектор, например, перене­сти вектор Ab в точку a. Однако перенести этот вектор “вне пространствен­ным” способом, т.е. игнорируя свойства про­странства, мы не можем. Следо­вательно, при обратном переносе и сопоставлении ис­ходного и перенесен­ного векторов оба вектора окажутся одинаковыми. Необходима другая про­цедура сравнения.

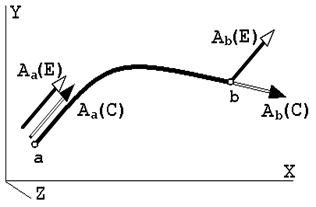
Рис.5

Обозначим криволинейное пространство символом C(ζ, η, ξ). Оно за­нимает бес­конечный объем. Теперь мы введем евклидово пространство E(x, y, z) в этом же беско­нечном пространстве. Таким образом, один и тот же бесконечный объем теперь описы­вается двумя способами: с помощью C и E. Эти пространства как бы “вложены” одно в другое. Мы предположим для упрощения, что между точками двух пространств имеет место взаимно однозначное соответствие.

Мы предлагаем другую процедуру сравнения векторов в криволиней­ном про­странстве. Мы выбираем в точке a два равных по величине и на­правлению вектора Aa(C) и Aa(E). Теперь мы перемещаем оба вектора в точку b. Вектор Aa(E) принадле­жит евклидовому пространству. Он будет пе­ремещаться параллельно самому себе: Aa(E) = Ab(E). Второй вектор будет перемещаться “параллельно самому себе” в пространстве C. Сравнивая век­тора Ab(E) и Ab(С) в точке b, мы можем определить величину кривиз­ны пространства C , как показано на рис. 5.

Итак, чтобы определить кривизну некоего пространства, мы должны иметь евклидово пространство, по отношению к которому и опреде­ляется кривизна ис­следуемого пространства. Математики знают об этом и всегда подразумевают наличие евклидова пространства в своих рассужде­ниях. Физики же упускают из внимания этот важный факт. Поэтому кривиз­на в их рассуждениях имеет абсолютный, а не относи­тельный смысл.

Проводя рассуждения, мы полагали, что координаты криволинейного простран­ства C выражены через координаты евклидового пространства E:

При наличии взаимно однозначного соответствия мы можем записать:

В системе координат пространства C прежнее евклидово пространст­во E будет выглядеть “криволинейным” по отношению к пространству C. В свою очередь, про­странство C будет иметь свойства евклидова пространст­ва.

Итак, для того, чтобы определить кривизну пространства:

A) мы должны иметь некоторое опорное евклидово пространство, по отноше­нию к которому и определяется кривизна;

B) опорное пространство должно иметь физический смысл и быть связано с ка­кими-либо явлениями материального мира;

C) найденная кривизна пространства не может иметь смысла абсолют­ной кри­визны; она характеризует кривизну одного пространства только по отношению к дру­гому.

D) остается "элементарный" вопрос: почему мы должны рассматри­вать криво­линейное пространство C в качестве реального пространства, а не евклидово простран­ство E, несмотря на то, что они равноправно описывают наше реальное пространство в рамках физических теорий и представле­ний?

Очевидно, мы никогда не сможем избавиться от евклидова простран­ства. Оно подобно тени преследует нас. Ньютон был глубоко прав, когда го­ворил о математиче­ском пространстве. Математическое пространство обладает протяженностью, изо­тропией и способно пронизывать все без исключения материальные объекты. Других свойств математическое про­странство не имеет.

Современные материалисты пишут, что физическое пространство не может быть пустым или чистым вакуумом. Однако они иногда совершают ошибку. Например, часть ученых утверждает, что пространство есть эфир, который имеет дополнитель­ные свойства по отношению к свойствам ма­тематического пространства (отождеств­ление пространства и эфира). Здесь можно согласиться с ними только в одном пункте. Пространство дей­ствительно не является пустым. Оно заполнено различными видами мате­риальной субстанции (эфир).

К сожалению, они иногда идут дальше. Свойства этой субстанции или эфира приписываются не материальному эфиру, а самому пространству. Благодаря такому шагу пространство превращается либо в материю или ма­териальный объект, либо в свойство материального эфира и т. д., или даже наоборот: материя в наших представ­лениях (но не на практике!) превраща­ется в функцию геометрии пространства.

 Скачать реферат