Теория и практика пассивной пеленгации и ее нераскрытые возможности

∆n

∆t3 = ∆T;

n∆

и альтернативные формулы: через пеленгационный угол движения (f1, f2) и курсовые углы (a1,a2,a3)

∆t1=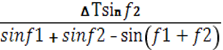или

∆t1= и т.д.

аналогично определяются Dt2 и Dt3

б) ; ;

и формула, для интереса, если известны моменты времени излучения сигналов (Тх, Тy, Т2,), то;

в) ; ;

;

и альтернативная формула, выраженная через коэффициенты m и n

α2=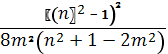

г) [Ty-Tx] = [Tz-Ty] =

д)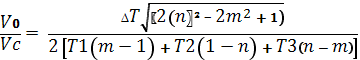

и альтернативная формула

е) ответить на этот пункт вопросов не составляет большой сложности, когда известны вышеопределенные параметры.

Задача 2.

Объекты "А" и "В", (самолеты) движутся прямолинейно-равномерно в пл. "Q".

Объект "В" непрерывно излучает сигналы которые объект "А" улавливает и фиксирует в моменты времени Т1, Т2, Т3 в дискретном режиме, т. е

Т2 - Т1 =Т3 - Т2 = t (Ty - Tx ¹ Т2 - Ty) (см. схем рис.2).

Рис. 2

По условию задачи известно:

отношение сигналов равно m и n, определенные аналогичным методом, как в выше приведенной задаче и заданы пеленгационые углы движения f1 и f2. По этим параметрам (f1, f2, m, n, T1, T2, T3), требуется ответить на все пункты предыдущих вопросов задачи 1, кроме пункта б, и дополнительно определить:

а) отношение скорости объекта "А" (Vo) к скорости объекта "В" (Vв)

т. е =?

б) отношение скорости объекта "В" к скорости сигнала (Vc), т. е =?

в) угол (a0), образованный пересечением траекторий движения объектов "А" и "В"

г) курсовые углы объектов "А" (α1, α2, α3) и "В" (β1,β2,β3)

д) время, когда расстояние между объектами будет минимальным, отсчет вести от момента времени первого приема сигнала (Т1).

Примечание 2. Здесь необходимо отметить, что некоторые формулы в постановке этой задачи, несколько видоизменяются, т.к. она по своей сложности расположена выше предыдущей. В то же время, когда рассматриваются взаимоотношения объектов произвольного движения при неизвестных начальных скоростях и ускорениях, то это уже другая ступень познания, требующая иного подхода соответствующих разъяснений математическими выкладками. Обратите особое внимание на отсутствие в этой теории таких физических параметров - как скорость сигнала (скорость света) и радиальной скорости объекта.

Задача 3

Система математических уравнений, выражающая взаимоотношения материальных тел методом пассивной пеленгации, складывается из множества неизвестных при минимальном количестве известных, причем уравнения не должны быть равносильными. Автору, этих строк, повезло, ему удалось составить систему уравнений таким образом, где количество неизвестных было на две единицы больше, чем самих уравнений. Начинать решать эту систему уравнений, по всем канонам математики, было бессмысленно. Однако, свершилось невероятное, при их разрешении, был найден всего лишь один неизвестный параметр, который стал исходной точкой математических преобразований нового содержания.

Современная навигационная наука нашла свой выход из этого положения, она стала вводить в свои уравнения известные параметры, которые эквивалентны неизвестным, извлекая их с навигационного пилотажного комплекса, так, например: неизвестные расстояния - через радиолокатор; путевую скорость, относительно земной поверхности - через доплеровский измеритель (ДИСС); воздушную скорость и высоту полета - через анероидно-мембранные приборы; ускорение через - акселерометры; курсовые углы - через гироскопические приборы и т.д.

Для обзорного сравнения, предлагаемого и существующего подхода к проблеме движения, рассмотрим наглядный пример и обратимся к рис.3.

Рис. 3.

Примечание: рисунок и формула t сбл. (1) скопированы из книги А.С. Карташкин. Авиационные радиотехнические системы который скопирован из книги А.С. Карташкин "Авиационные радиосистемы" (Издательское предприятие Радио СОФТ Москва 2007г). Глава 3. Радиосистемы навигационно-пилотажного комплекса, раздел 3.5 - Радиосистемы предупреждения столкновений.

Очень коротко, на рисунке 3 обозначены все основные навигационные параметры, присущие этому движению. Постановочные условия этой задачи аналогичны задаче № 2 и требуется определить время сближения, когда расстояние между конфликтующими самолетами будет минимальным. Методом несложных расчетов, используя принцип относительности и все обозначенные на рисунке параметры, которые извлекаются из соответствующего навигационного оборудования, выводится формула времени сближения (tсбл). В окончательном виде она выглядит так:

tcбл =(1)

Эта формула выведена без использования скорости сигнала, т. е она представлена как мгновенная. А теперь сравним эту формулу (1), с альтернативными (2), (3), (4) выведенные аналитическим способом, используя природные свойства пассивной пеленгации, они так же представлены по мгновенной скорости сигнала.

(2)

tcбл = (3)

(4)

Отсчет времени сближения идет с момента времени приема первого сигнала (Т1).

Задача 4

В плоскости Q объекты "О" и "В" находятся в неподвижном состоянии, а объект "С" движется прямолинейно-равномерно и непрерывно излучает сигналы. Наблюдатель, объекта "О", в момент времени Т1 измеряет угол элонгации (Э1) между объектами С и В и фиксирует энергию сигналов, приходящего с объекта С и отраженную энергию от объекта В, условно принимая энергию сигнала от объекта С за эталон измерения (см. схем. рис.4).

 Скачать реферат