Расчет характеристик и переходных процессов в электрических цепях
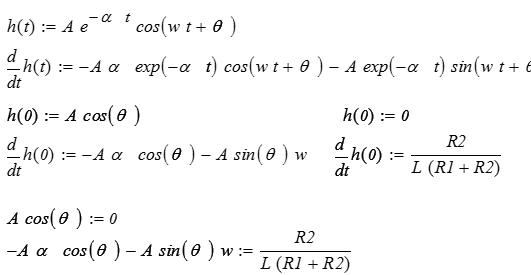
Учтя всё это можно составить систему уравнений:


Решение системы уравнений и подстановка данных приводит к значению:
Переходная характеристика после подстановки значений имеет вид:
или
Её график изображен на рисунке 2.3. Расчетные данные находятся в приложении А.
Рисунок 2.3 – График зависимости переходной характеристики 3. НАХОЖДЕНИЕ ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ ЦЕПИ Импульсная характеристика вычисляется с помощью зависимости от В импульсной характеристике отсутствует дельта функция, поскольку После подстановки значений:
получим
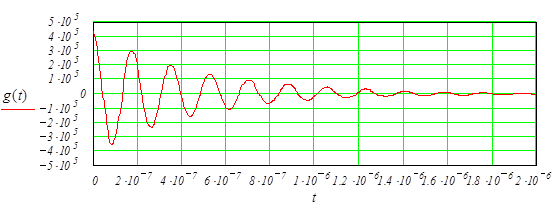
График импульсной функции изображен на рисунке 3.1. Расчетные данные находятся в приложении А.
Рис.3.1 – График зависимости импульсной функции 4. ОПРЕДЕЛЕНИЕ КОМПЛЕКСНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ ЦЕПИ Комплексный коэффициент передачи может быть представлен в показательной форме записи:
где Модель комплексного коэффициента передачи представляет собой АЧХ цепи, а аргумент - ФЧХ цепи. Его можно найти из соотношения:
Напряжение на резисторе R2 равно напряжению на индуктивности L.
Выходя из этого, можно записать:
Комплексный коэффициент передачи при этом:
Выделим мнимую часть числа и найдём модуль (АЧХ):
Подставим значения в выведенные формулы и получим:
Аргумент Графики АЧХ , ФЧХ представлены на рисунках 4.1и 4.2 соответственно
Рисунок 4.1 -АЧХ
Рисунок 4.2 – ФЧХ
5. НАХОЖДЕНИЕПЕРЕДАТОЧНОЙ ФУНКЦИИ Формально выражения для комплексного коэффициента передачи Произведём замену:
Подставив значение
получим:
Умножим и поделим, прибавим и отнимем комплексно сопряженные числа:
Сведём по формуле квадратов:
Подставив числовые значения и сделав еще некоторые преобразования получим:
Зная, что
запишем импульсную характеристику:
Зная, что
получим переходную характеристику:
Полученные выражения для 6. РАСЧЕТ ОТКЛИКА ЦЕПИ НА ПРОИЗВОЛЬНОЕ, ПОСТРОЕНИЕ ГРАФИКА ОТКЛИКА
Опишем входной сигнал (напряжение) с помощью простой функции:
Учитывая то, что вид реакции цепи - iL запишем на каждом временном интервале функцию тока через напряжение:
ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы были изучены классический и операторный методы нахождения временных характеристик. Классический метод оказался более прост, так как требовал меньше математических выкладок, для определения Также были приобретены практические навыки применения интегралов наложения для расчета переходных процессов и прохождения простейших сигналов через цепи.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Основы теории цепей: Методические указания к курсовой работе для студентов – заочников специальности 23.01 "Радиотехника"/ Сост. Коваль Ю.А., Праги О.В. – Харьков: ХИРЭ, 1991. – 63 с.
![]()


![]()
![]() С ИСПОЛЬЗОВАНИЕМ ЕЕ СВЯЗИ С
С ИСПОЛЬЗОВАНИЕМ ЕЕ СВЯЗИ С ![]() , ПОСТРОЕНИЕ ГРАФИКА
, ПОСТРОЕНИЕ ГРАФИКА ![]()
![]() по формуле:
по формуле:
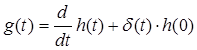 (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() .
.
![]()
![]()
![]()
![]() , ПОСТРОЕНИЕ ГРАФИКОВ АЧХ И ФЧХ
, ПОСТРОЕНИЕ ГРАФИКОВ АЧХ И ФЧХ
![]() , (4.1)
, (4.1)
![]() - модуль комплексного коэффициента передачи;
- модуль комплексного коэффициента передачи;
![]() - аргумент комплексного коэффициента передачи.
- аргумент комплексного коэффициента передачи.



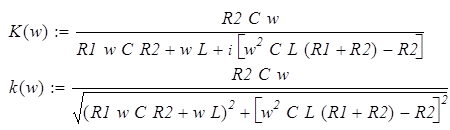
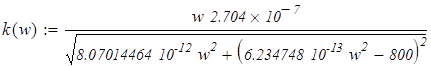
![]() комплексного коэффициента передачи (аргумент - ФЧХ цепи):
комплексного коэффициента передачи (аргумент - ФЧХ цепи):
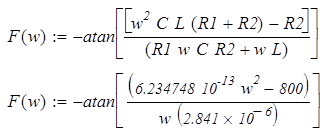


![]() И УСТАНОВЛЕНИЕ ЕЕ СВЯЗИ С
И УСТАНОВЛЕНИЕ ЕЕ СВЯЗИ С ![]() И
И ![]()
![]() и передаточной функцией
и передаточной функцией ![]() отличаются только переменной
отличаются только переменной ![]() для
для![]() и
и![]() для
для ![]() .
.

![]()

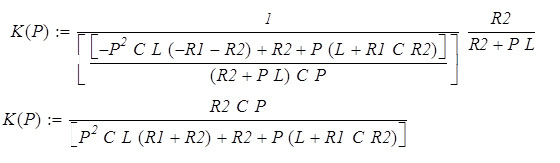



![]()
![]()


![]() и
и![]() совпадают с определенными в п.2 и п.3.
совпадают с определенными в п.2 и п.3.
![]()
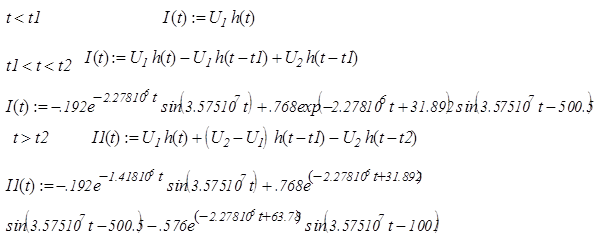
![]() и
и ![]() . Временные характеристики, найденные этими двумя методами совпали. Был применен комплексный метод для нахождения частотных характеристик цепи.
. Временные характеристики, найденные этими двумя методами совпали. Был применен комплексный метод для нахождения частотных характеристик цепи.
Другие рефераты на тему «Коммуникации, связь и радиоэлектроника»:
Поиск рефератов
Последние рефераты раздела
