Одномерная оптимизация функций методом золотого сечения

function Maximum(a,b,eps)

%Maximum(a,b,eps) функция нахождения максимума функции f(x)

% методом "золотого сечения" на отрезке [a, b] с точностью eps.

% Функция f(x) задаётся в M-файле, находящимся в той же дирекктории.

% (!) Для правильной работы функции необходимо, чтоб a<b и

% искомое значение было б единствено на [a, b].

%---------------------------------

-----------

% Построим график (необязательно)

x=a:0.001:b; y=f(x);

plot(x,y,'k',a,f(a),'.b',b,f(b),'.b');

text(a,f(a),'A','FontSize',15); text(b,f(b),'B','FontSize',15);

title('График функции f(x).');

xlabel('Ось x.'); ylabel('f(x)');

grid on; hold on;

%--------------------------------------------

k1=(sqrt(5)-1)/2; k2=1-k1;

x1=k1*a+k2*b; x2=k2*a+k1*b;

A=f(x1); B=f(x2);

while 1

if A>B

b=x2;

if b-a<eps break;

else x2=x1; B=A; x1=k1*a+k2*b; A=f(x1);

end;

else

a=x1;

if b-a<eps break;

else x1=x2; A=B; x2=k2*a+k1*b; B=f(x2);

end;

end;

end;

x=(a+b)/2;

tab=strcat('%.',int2str(abs(floor(log10(eps)))),'g');

%(!) здесь задаётся точность результата(сколько цифр после запятой)

% и формат вывода, сравни Minimum

disp(sprintf(strcat('%s',tab),'Максимум функции f(x): x_max = ',x));

%-----------------------------------

%выведем результат на график

plot(x,f(x),'or'); text(x,f(x),'X_{max}','FontSize',15);

Б. Программа вычисления минимума:

function Minimum(a,b,eps)

%Minimum(a,b,eps) функция нахождения минимума функции f(x)

% методом "золотого сечения" на отрезке [a, b] с точностью eps.

% Функция f(x) задаётся в M-файле, находящимся в той же дирекктории.

% (!) Для правильной работы функции необходимо, чтоб a<b и

% искомое значение было б единствено на [a, b].

k1=(sqrt(5)-1)/2; k2=1-k1;

x1=k1*a+k2*b; x2=k2*a+k1*b;

A=f(x1); B=f(x2);

while 1

if A<B

b=x2;

if b-a<eps break;

else x2=x1; B=A; x1=k1*a+k2*b; A=f(x1);

end;

else

a=x1;

if b-a<eps break;

else x1=x2; A=B; x2=k2*a+k1*b; B=f(x2);

end;

end;

end;

x=(a+b)/2;

disp(sprintf('%s %.15f','Минимум функции f(x): x_min = ',x));

3.2 Руководство программиста

Запускается файл Example.m, она вызывает 2 функции максимум и минимум. Функция максимум вычисляет максимум В функцию максимум передаётся промежуток, в которой нужно вычислить максимум…В первых строках строится график заданной функции. Цикл while – бесконечный цикл. Он останавливается только, если у нас погрешность вычисленного значения меньше заданного eps. Потом задаётся точность результата (сколько цифр после запятой) и формат вывода.

Функция минимум вычисляет минимум… В функцию минимум передаётся промежуток, в которой нужно вычислить минимум … Цикл while – бесконечный цикл. Он останавливается только, если у нас погрешность вычисленного значения меньше заданного eps. Потом задаётся точность результата(сколько цифр после запятой) и формат вывода.

3.3 Руководство пользователя

Для того, чтобы вычислить максимум и минимум необходимо открыть файл Example.m, ввести промежутки вычисления минимума и максимума, задать eps и нажать Run (F5). После чего программа построит график заданной функции и вычислит максимум и минимум.

3.4 Описание всех использованных в программе встроенных функций MatLab

В программе использовались встроенный функции: plot, grid on, abs, disp, hold on.

plot – функция построения графиков.

disp — функция, выводящая текстовые данные.

grid on – функция включения отображения сетки, которая строится пунктирными линиями.

abs – возвращает абсолютную величину для каждого числового элемента вектора x.

hold on – обеспечивает продолжение вывода графиков в текущее окно, что позволяет добавлять последующие графики к уже сеществующим.

Описание встроенных функций MatLab помогающих облегчить решение систем уравнений

Важной задачей численных методов – поиск минимума функций f(x) в некотором интервале изменения x – от x1 до x2. Если нужно найти максимум такой функции, то достаточно поставить знак "минус" перед функцией. Для решения этой задачи используется следующая функция:

- fmin (‘ fun’, x1, x2) возвращает значение x, которое является локальным минимумом функции funx на интеравле x1<x<x2;

- fmin (‘ fun’, x1, x2, options) – сходна с описанной выше функцией, но использует контрольные параметры options для управления процессом по умолчанию;

- [x, options] = fmin(…) дополнительно возвращает вектор контрольных параметров options, в десятом столбце которого содержится число выполненных итераций.

В этих представлениях используются следующие обозначения: x1, x2 – интервал, на котором ищется минимум функции; P1, P2…- передаваемые в функцию аргументы; fun – строка, содержащая название функции, которая будет минимизирована; options – вектор контрольных параметров, имеющий 18 компонентов. Только три из них используются функцией fmin: options(1) – при ненулевом значении отображаются промежуточные шаги решения, options (2) задает итерационную погрешность, по умолчанию она равна 1.е-4, и options (14) задает максимальное число итераций, по умолчанию равное 500.

3.5.Распечатка серии тестов

Проведем серию тестов, решив приведенные выше системы в заданиях для тестовых расчетов, используя написанную программу .

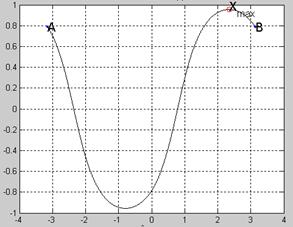
а). Запускаем example.m для функции f(x) = в промежутке [-4,4].

Максимум функции f(x): x_max = 4

Минимум функции f(x): x_min = 0.000000005266636

График функций

б) Запускаем example.m для функции f(x) = arctg(sinx- cosx) в промежутке (-3.14, 3.14);

Максимум функции f(x): x_max = 2.35619

Минимум функции f(x): x_min = -0.785398139394453

График функций

в) Запускаем example.m для функции f(x) = +x2 в промежутке (0, 20)

3.6 Анализ полученных результатов

В ходе курсовой работы мною были изучены некоторые аспекты программирования в среде MATLAB, а также некоторые встроенные функции данного пакета. При оформлении курсовой работы был получены навыки оформления программной документации в соответствии с Единой Системой Программной Документации, а также большой практический опыт работы в MATLAB, Microsoft Word 2003, (хотя освоение этих программных продуктов не было целью курсовой работы, данные навыки нельзя считать бесполезными). Теоретические сведения были закреплены практическими занятиями.

4. Список использованной литературы

1. Численные методы. Волков Е.А.: Учебное пособие. – М.: Наука. Главная редакция физико-математической литературы, 1982.

2. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. – СПб.: Питер, 2002.

 Скачать реферат