Анализ структурной схемы надежности
13. Гипотезами являются Н1=х1х6х5х20, Н2=х1х6х5х20,, Н3=х6,х5, Н4=х6,х5,,
Н5=х1,х5, Н6=х1,х5,.
14. Перейдем от функции алгебры логики к вероятностной функции, то есть от структурной функции y(x) к функции надежности
h(r):r5-r4+2r3+r2-2r
15. Так как система состоит из невосстанавливаемых элементов, то элементами функции надежности являются вероятности безотказной работы. В качест
ве математической модели надежности выберем экспоненциальную модель.
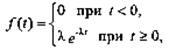
Функция распределения F (t) = Р(Т<t) определяет вероятность отказа за время длительностью t и называется функцией ненадежности.
На практике длительность времени безотказной работы элемента часто имеет показательное распределение с функцией распределения:
F (t) = 1-e-λt.
16. На основе исходных данных (интенсивностей отказов) составим таблицу значений вероятности безотказной работы таким образом, чтобы вероятность безотказной работы системы изменялась в диапазоне от 0,95 до 0,2 (табл.2).
Таблица 2. Значения вероятности безотказной работы.
|
Номер |
|
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
|
1 |
12 |
0,548812 |
0,30119421 |
0,16529889 |
0,09071795 |
0,049787 |
0,027324 |
0,014996 |
|
2 |
11 |
0,57695 |
0,33287108 |
0,19204991 |
0,11080316 |
0,063928 |
0,036883 |
0,02128 |
|
3 |
10 |
0,606531 |
0,36787944 |
0,22313016 |
0,13533528 |
0,082085 |
0,049787 |
0,030197 |
|
4 |
3 |
0,860708 |
0,74081822 |
0,63762815 |
0,54881164 |
0,472367 |
0,40657 |
0,349938 |
|
5 |
10 |
0,606531 |
0,36787944 |
0,22313016 |
0,13533528 |
0,082085 |
0,049787 |
0,030197 |
|
6 |
7 |
0,704688 |
0,4965853 |
0,34993775 |
0,24659696 |
0,173774 |
0,122456 |
0,086294 |
|
7 |
8 |
0,67032 |
0,44932896 |
0,30119421 |
0,20189652 |
0,135335 |
0,090718 |
0,06081 |
|
8 |
15 |
0,472367 |
0,22313016 |
0,10539922 |
0,04978707 |
0,023518 |
0,011109 |
0,005248 |
|
9 |
1 |
0,951229 |
0,90483742 |
0,86070798 |
0,81873075 |
0,778801 |
0,740818 |
0,704688 |
|
10 |
18 |
0,40657 |
0,16529889 |
0,06720551 |
0,02732372 |
0,011109 |
0,004517 |
0,001836 |
|
11 |
12 |
0,548812 |
0,30119421 |
0,16529889 |
0,09071795 |
0,049787 |
0,027324 |
0,014996 |
|
12 |
11 |
0,57695 |
0,33287108 |
0,19204991 |
0,11080316 |
0,063928 |
0,036883 |
0,02128 |
|
13 |
13 |
0,522046 |
0,27253179 |
0,14227407 |
0,07427358 |
0,038774 |
0,020242 |
0,010567 |
|
14 |
2 |
0,904837 |
0,81873075 |
0,74081822 |
0,67032005 |
0,606531 |
0,548812 |
0,496585 |
|
15 |
4 |
0,818731 |
0,67032005 |
0,54881164 |
0,44932896 |
0,367879 |
0,301194 |
0,246597 |
|
16 |
8 |
0,67032 |
0,44932896 |
0,30119421 |
0,20189652 |
0,135335 |
0,090718 |
0,06081 |
|
17 |
10 |
0,606531 |
0,36787944 |
0,22313016 |
0,13533528 |
0,082085 |
0,049787 |
0,030197 |
|
18 |
10 |
0,606531 |
0,36787944 |
0,22313016 |
0,13533528 |
0,082085 |
0,049787 |
0,030197 |
|
19 |
12 |
0,548812 |
0,30119421 |
0,16529889 |
0,09071795 |
0,049787 |
0,027324 |
0,014996 |
|
20 |
15 |
0,472367 |
0,22313016 |
0,10539922 |
0,04978707 |
0,023518 |
0,011109 |
0,005248 |
|
Р |
|
0,996113 |
0,64044938 |
0,55029007 |
0,4367876 |
0,317304 |
0,298063 |
0,211081 |
Скачать рефератДругие рефераты на тему «Программирование, компьютеры и кибернетика»:
Поиск рефератов
Последние рефераты раздела
- Основные этапы объектно-ориентированного проектирования
- Основные структуры языка Java
- Основные принципы разработки графического пользовательского интерфейса
- Основы дискретной математики
- Программное обеспечение системы принятия решений адаптивного робота
- Программное обеспечение
- Проблемы сохранности информации в процессе предпринимательской деятельности