Тяготение

НЬЮТОНОВСКАЯ ТЕОРИЯ ГРАВИТАЦИИ И ДВИЖЕНИЕ В СОЛНЕЧНОЙ СИСТЕМЕ

Чтобы начертить окружность радиуса r с центром в точке S, нужно закрепить один конец нити в S, а к другому привязать карандаш Р. Длина нити - это радиус r. Держа нить натянутой, ведем карандашом по бумаге, и он вычерчивает окружность. А как вычертить эллипс с фокусами в точках S и S' и большой полуосью а? Тут построение немного с

ложнее (рис. 1.4). Возьмем кусок нити длиной 2а и закрепим ее концы в S и S'. Будем вести карандашом так, чтобы его конец Р скользил вдоль нити, а участки PS и PS' были все время натянуты. При построении окружности конец карандаша все время остается на расстоянии PS = а; в случае эллипса PS + PS' = 2а. Ясно, что при построении эллипса расстояние SS' не может превышать 2a. Когда S и S' совпадают, эллипс превращается в окружность.

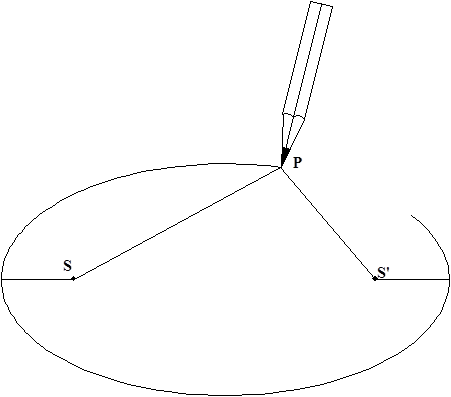
Рисунок 1.4. Простой способ построения эллипса.

Ньютон применил свою динамику для описания движения планет под действием тяготения Солнца. Его уравнения движения (см. гл. 1) связывают ускорение планеты с приложенной силой, в данном случае - с силой тяготения. Можно ли, зная ускорение планеты, рассчитать ее траекторию в пространстве? Для решения этой задачи Ньютон создал новый раздел математики, который он назвал флюксиями и который теперь называется математическим анализом. При помощи методов анализа ему удалось доказать, что планеты движутся по эллиптическим траекториям и подчиняются трем законам Кеплера. Но научное сообщество всегда склонно к консерватизму и с подозрением относится к новым методам. Поэтому, чтобы сделать теорию более доступной. Ньютон придал своим простым аналитическим доказательствам более привычную, хотя и более громоздкую, геометрическую форму. В книге Ньютона “Математические начала натуральной философии”, опубликованной в 1687 г., содержится его знаменитая работа о движении и гравитации.

Можно понять, как из законов Кеплера вытекает закон обратной пропорциональности квадрату расстояния для гравитации, и не прибегая к тонким математическим рассуждениям. Рассмотрим упрощенную задачу движения по окружности, которая, как отмечалось выше, является частным случаем эллипса.

На рис. 1.5 изображена планета Р массы т, которая движется по окружности с центром S, где находится Солнце. Прежде всего отметим, что, поскольку радиус SP описывает равные площади за равные промежутки времени (второй закон Кеплера), точка Р должна двигаться по окружности с постоянной по величине скоростью.

Рисунок 1.5. Поскольку планета Р движется по круговой орбите, а Солнце находится в центре, то сила взаимодействия между Солнцем и планетой и центростремительно ускорение направлены по радиусу.

Пусть радиус круга равен r, тогда длина окружности равна 2πr. Если период обращения планеты равен Т, то постоянная величина скорости v выражается так:

.

В каком направлении должна действовать сила на планету Р, чтобы она двигалась по окружности? Утверждать, что сила действует в направлении движения, значит, впадать в ту же ошибку, что Аристотель и его последователи. Сила связана не со скоростью, а с ускорением. А ускорение точки Р направлено к центру S и равно по величине v2/r (см. гл. 1). Поэтому сила F, действующая на планету, направлена к центру и вычисляется по второму закону Ньютона: сила равна произведению массы на ускорение, или

Поскольку v = 2πr/T, имеем

.

Воспользуемся теперь третьим законом Кеплера, который гласит, что Т2 пропорционально r3, т.е.

T2 = kr3,

где k - некоторое постоянное число. Подставляя T2 в выражение для силы F, получаем

Отсюда следует, что сила, действующая на планету Р, уменьшается обратно пропорционально квадрату ее расстояния от солнца.

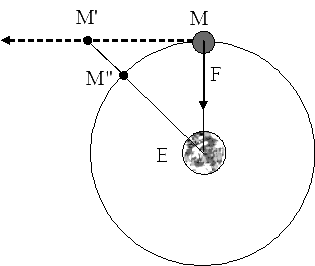
Рисунок 1.6. Если б гравитационное взаимодействие исчезло, то Луна полетела бы по прямой (касательной к кругу).

Закон тяготения описывает не только движение планет вокруг Солнца, но и движение Луны вокруг Земли, а также движение других спутников вокруг своих планет. Поначалу может показаться удивительным, что один и тот же закон управляет и падением яблока, и движением Луны. Внимательно изучив рис. 1.6, нетрудно понять, что Луна (как и яблоко) тоже падает на Землю, но только непрерывно. Пусть Луна М движется по окружности с центром в Земле Е. Вообразим, что сила притяжения Земли вдруг по волшебству исчезает. Как показано на рис. 1.6, Луна будет тогда двигаться вдоль штриховой прямой с постоянной скоростью - ведь никакая сила на нее не действует (первый закон Ньютона)! Сравним этот путь с фактической круговой траекторией Луны вокруг Земли. Предоставленная себе самой. Луна, естественно, стремилась бы улететь вдоль штриховой прямой, но Земля постоянно “тащит” Луну к себе. Поэтому можно рассматривать движение Луны как непрерывное падение на Землю. Правда, обладая поперечной скоростью, она никогда не достигает Земли, а смещается перпендикулярно прямой Земля-Луна.

КТО ПЕРВЫМ ЗАДУМАЛСЯ О ГРАВИТАЦИИ?

Ньютон не был первым, кто задумался о гравитации. Еще в XV в. некоторым астрономам приходила в голову мысль о существовании притяжения между небесными телами и Землей. Утверждалось, что Земля притягивается во всех направлениях “магнетическими” силами, но, поскольку эти силы во всех направлениях одинаковы. Земля остается в покое.

Легенда о яблоке приписывает Ньютону открытие гравитации в 1666 г., хотя первая его публикация о ней, трактат “Propositions de Motu”, был прочитан в Королевском обществе в феврале 1685 г., а сами “Начала” были изданы в 1687 г. Между тем в 1674 г. Роберт Гук опубликовал свою работу, в которой движение Земли вокруг Солнца описывалось при помощи закона притяжения, которое убывало с расстоянием. Рассказывают, будто Гук сообщил о своих идеях Ньютону, который независимо пришел к похожим выводам.

Почему Ньютон ждал так долго, почти два десятилетия, прежде чем опубликовал свои результаты? В нынешнюю эпоху в науке, для которой подходит лозунг “публикуй или погибай” и скоропалительная публикация полусырых результатов - довольно распространенное явление, понять сдержанность Ньютона еще труднее.

Утверждают, что Ньютон был педантом и хотел повременить до тех пор, пока не разберется с некоторыми проблемами, связанными с его теорией. Одной из этих проблем была необходимость математически доказать, что сферическое тело притягивает другие тела так, как если бы вся его масса была сосредоточена в центре . Другая проблема была связана с наблюдениями. По-видимому, Ньютон хотел дождаться появления надежных измерений расстояний в системе Земля — Солнце - Луна, чтобы проверить правильность своей теории. Они появились в конце 1670-х годов. Только тогда Ньютон почувствовал уверенность в своем законе тяготения.

 Скачать реферат