Установка для определения релаксационных характеристик низкомодульных полимерных материалов

Наиболее полную информацию о релаксационных свойствах резин дает временная зависимость модуля упругости E(t), типичный вид которой представлен на рис. 1 [1]. Как видно из рисунка, имеются три области, описывающие деформационные свойства резины с характерными значениями модулей упругости: I – область стеклообразного состояния с модулем Ес, II – переходная область с модулем, меняющемся от Ес до н

ачального значения высокоэластичного (равновесного) модуля и III – область высокоэластичности, в которой происходит медленная физическая релаксация, по завершению которой материал характеризуется значением равновесного модуля упругости Ер. [1]. При этом ход кривой Е = f(lgt) для различных полимеров, в зависимости от химической природы и технологических особенностей изготовления будет различным и обусловлен характерными релаксационными процессами, происходящими в материале.

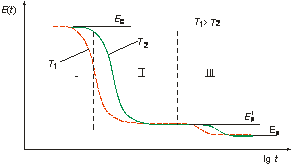
Рис. 1. Временная зависимость модуля упругости E(t).

Согласно теории температурно-временной эквивалентности, нагревание полимерных материалов приводит к параллельному смещению кривой Е=f(lgt) в область меньших значений времени [2]. При этом в большей степени проявляются более медленные процессы релаксации (рис. 1). Совершенно очевидно, что варьируя временем воздействия и температурой, можно получать релаксационные кривые модуля упругости в широком диапазоне. Такой подход даёт ценную информацию о вязкоэластических свойствах НП.

Для этих целей предлагается использовать метод динамического индентирования, который разработан в ИПФ НАН Беларуси и реализован в приборе ИМПУЛЬС 1Р [3] (рис. 2). Данный метод заключается в нанесении удара жестким индентором (бойком) по испытуемому материалу и непрерывной регистрации процесса контактного взаимодействия индентора с материалом. Исходной информацией о свойствах материала является массив текущей скорости перемещения индентора V(t) в контакте с материалом. Дифференцирование скорости с последующим умножением на массу индентора позволяет получить текущее значение контактного усилия P(t), а интегрирование – значение перемещения α(t). Наиболее интересной для анализа является зависимость контактное усилие-глубина внедрения индентора, которую можно получить, исключив время как параметр из соответствующих кривых. Данная зависимость состоит из двух характерных этапов: первый этап (активная часть удара) – этап нагружения материала, при котором индентор внедряется в материал и достигает своего максимального перемещения αмакс, и второй (пассивная часть удара) – этап разгрузки, на котором происходит отскок индентора и восстановление отпечатка.

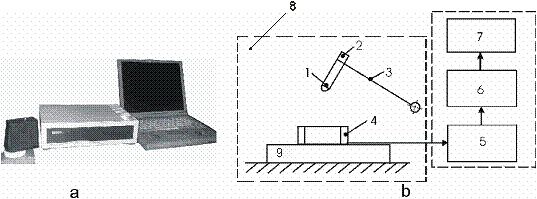
Рис. 2. а – общий вид прибора ИМПУЛЬС 1Р. b- блок-схема установки: 1- индентор, 2- магнит, 3- поворотный рычаг, 4- индукционный датчик, 5 –предварительный усилитель, 6 – аналого-цифровой преобразователь, 7 –персональный компьютер, 8 – термокамера; 9 – испытуемый образец.

Прибор ИМПУЛЬС-1Р позволяет определять релаксационный динамический модуль упругости Eр на любом этапе удара, а также ряд других параметров материала, характеризующих релаксационные свойства: вязкость h, эластичность, тангенс угла механических потерь tg δ [3]. При импульсном нагружении материал проявляет вязкие свойства, которые невозможно оценить при статическом воздействии, кроме того, динамическое нагружение моделирует наиболее жесткие условия, которым может подвергаться материал во время эксплуатации [4].

Диоксид кремния SiO2 может существовать во множестве различных кристаллических форм (α- и β-кварц, α- и β-кристобалит и др). Большинство из этих структур образовано из тетраэдров с атомом кремния в центре и атомом кислорода в углах. Эти структуры слабо различимы по энергии и отличаются друг от друга главным образом способом соединения тетраэдров. Хотя строение большинства разновидностей диоксида кремния хорошо изучено, структура β-кристобалита до сих пор не ясна (существует, по меньшей мере, пять вариантов). Структуру β-кристобалита часто называют «идеальным» β-кристобалитом так как она имеет высокую симметрию. Элементарная ячейка β-кристобалита содержит две формульные единицы SiO2. Реальная структура β-кристобалита может быть представлена как результат разворота на ±20º каждого тетраэдра SiO4 из идеальной структуры вокруг оси четвертого порядка. Это приводит к изменению кубической симметрии в тетрагональную с пространственной группой и двумя формульными единицами SiO2 в элементарной ячейке [1,2]. Характеристическими параметрами кристаллической структуры подобной халькопириту являются параметры решетки (а и с), тетрагональное сжатие (γ=с/а=1.577), смещение анионов из узлов ГЦК подрешетки (х=0.1234, в единицах a), угол разворота тетраэдров φ=20º и валентный угол θ(O-Si-O)=147.6º.

Соединения LiBO2 [3], NaPN2 и LiPN2 [4] со структурой халькопирита имеют изоэлектронное сходство с семейством халькопирита (16 электронов в элементарной ячейке) и одновременно являются кристаллохимическими аналогами β-кристобалита. Основными особенностями этой группы кристаллов являются: сильное тетрагональное сжатие 1.403, 1.55 и 1.56; большое смещение анионов 0.1239, 0.1574 и 0.1669, в единицах a; угол разворота тетраэдров φ 26.4º, 32º и 34.2º, валентные углы 137.4º, 128.7º и 125.4º; для NaPN2, LiBO2 и LiPN2, соответственно.

Целью настоящей работы является расчет из первых принципов в рамках функционала локальной электронной плотности электронной структуры соединений SiO2, NaPN2, LiBO2 и LiPN2 с решеткой халькопирита. В расчетный базис включались псевдоатомные sp3d5-орбитали каждого атома. Сходимость по полной энергии обеспечивалась не хуже 0.001 а.е. Вычисление зонной структуры всех соединений проводилось в точках высокой симметрии Т(0,0,1), Г(0,0,0), N(0.5,0.5,0), P(0.5, 0.5, 0.5) в единицах () и вдоль линий их соединяющих. Были вычислены также плотность состояний N(E) и распределение заряда валентных электронов ρ(r).

Результаты вычислений зонной структуры и плотности состояний ряда соединений SiO2, NaPN2, LiBO2 и LiPN2 представлены на рис.1. За начало отсчета шкалы энергий выбрано положение последней заполненной валентной зоны. Валентная зона SiO2 состоит из четырех разрешенных энергетических полос, что не характерно для соединений со структурой халькопирита, валентная зона которых имеет три разрешенных полосы энергий. Вторая связка валентных зон включает четыре ветви, а не две, как в халькопиритах. Вершина валентной зоны SiO2 реализуется в точке Т и следовательно кристалл является непрямозонным.

Структура валентной зоны LiBO2 во многом подобна структуре валентной зоны SiO2. Основное отличие этих соединений сосредоточено в строении вершины валентной зоны, где абсолютный максимум располагается в точке Г, а в точках T и N имеются локальные максимумы. По этой причине LiBO2 следует отнести к прямозонным соединениям.

 Скачать реферат