Условия фильтрации для реактивных лестничных четырехполюсников
Реактивный четырехполюсник называют лестничным, если образующие его РД поочередно включаются в продольные и поперечные ветви схемы.
Лестничные четырехполюсники образуют из Т- и П- образных четырехполюсников путем каскадного согласованного соединения их. Последние же получают путем соединения элементарных Г- образных полузвеньев Т- или П- образными сторонами, как показано на рисунках:
Г - образное Симметричное Симметричное полузвено Т - образное звено П - образное звено
Рассмотрим условия фильтрации для Г- образного полузвена.
Условия фильтрации для реактивных четырехполюсников
Определим условия, при которых реактивный четырехполюсник (четырехполюсник без потерь) будет электрическим фильтром, т.е. устройством, имеющим в некоторой области частот полосу пропускания, а в другой - полосу задерживания.
Условия фильтрации (УФ) найдем для четырехполюсника в виде элементарного Г- образного полузвена, а затем распространим их на каскадное соединение, т.е. на Т- и П- образные звенья.
Ранее было получено соотношение, связывающее характеристическое затухание с параметрами XX и КЗ.
Для Г- образного полузвена найдем:
С учетом этого можно записать выражение для характеристического затухания Г- образного полузвена:
Как видно из формулы, характеристическое затухание зависит от соотношения сопротивлений продольной и поперечной ветвей четырехполюсника. Условились характеристической ПП считать область частот, где характеристическое затухание равно нулю.
Следовательно, в области частот, в которой модуль выражения (1) равен 1, ln=0 и фильтр имеет ПП. При всех же других частотах ac Не трудно заметить, что модуль выражения (1) равен 1 в двух случаях:
а) при Если обозначить Таким образом, ПП реактивного четырехполюсника расположена на частотах, на которых справедливо неравенство
Видно, что данное неравенство имеет место при выполнении двух условий:
1. 2. Фактически это и есть условие фильтрации (т.е. условие получения ПП) для реактивного Г- образного полузвена.
При составлении звеньев и более сложных фильтров из Г- образных полузвеньев, имеющих одинаковую частоту среза, затухание суммируется, следовательно условия фильтрации определяются Г- образным полузвеном.
Рассмотрим примеры применения УФ:
1) Данный четырехполюсник - ФНЧ.
Из графика видно, что условия фильтрации выполняются в полосе частот (0,ω0) поэтому данный четырехполюсник является ФНЧ.
Если L и С поменять местами, то нетрудно убедиться, что четырехполюсник будет ФВЧ.
2) Данный четырехполюсник - ПФ.
Определим условия фильтрации для мостового реактивного четырехполюсника.
Ранее мы установили, что ХПП лежит в области частот, где
В данном случае Полученное выражение будет отрицательным при противоположных знаках Za и Zb.
Таким образом ХПП для мостового симметричного четырехполюсника лежит в области частот, где Za и Zb имеют противоположные знаки.
Укажем, что мостовые звенья используются при построении фазовых корреляторов, кварцевых фильтров и других устройств.
Заключение
Отметить, что использование характеристических параметров для получения условий фильтрации дает возможность сравнительно легко определить тип фильтра и примерное расположение полос пропускания и задержания. Однако расчет фильтра по характеристическим параметрам является не оптимальным и не обладает должной гибкостью. Поэтому на практике все более широкое применение находят так называемые методы синтеза электрических фильтров по их рабочим параметрам, что и будет продемонстрировано в следующих лекциях.
Литература
1. Белецкий А.Ф. «Теория линейных электрических цепей » Москва 1986 с 368-383
2. Белецкий А.Ф. «Линейные устройства аппаратуры связи. Конспект лекций» 3. Бакалов В.П. «Теория электрических цепей» Москва «Радио и связь» 1998- с.368-390


 (1)
(1)
![]()
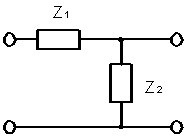
 (1)
(1)
![]() 0 т.е. расположена ПЗ.
0 т.е. расположена ПЗ.
 б) при
б) при 
![]()
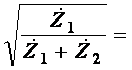 jA то
jA то
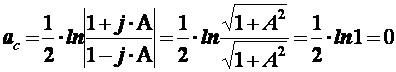
 ;
;  ;
; 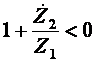 ;
;  ;
;
![]() и
и ![]() должны иметь разные знаки;
должны иметь разные знаки;
![]()
![]()






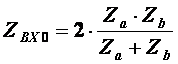 и
и 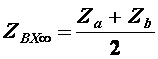 откуда
откуда 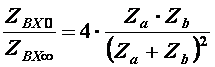
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
