Уравнения Больцмана, Лиувилля, Боголюбова

Рефераты / Физика и энергетика / Уравнения Больцмана, Лиувилля, Боголюбова

Введем с этой целью n-частичные функции распределения

. (4)

Эти функции подчинены следующему из (1) условию нормировки:

, (5)

и если мы придаем вероятностный смысл функции F(N) (х1, ,xN, t),

то и функции приобретают статистическую интерпретацию. Здесь и в дальнейшем мы опускаем для краткости индекс (N) в обозначении F(nN). Выражение представляет собой вероятность того, что первые п частиц системы (а не ансамбля систем!) имеют координаты и скорости, лежащие в пределах (ri, ri + dri), (vi, vi + dvi).

Выведем систему дифференциальных уравнений, которым подчиняются функции . Умножим с этой целью уравнение (2) на и проинтегрируем полученное равенство, пользуясь выражением (3):

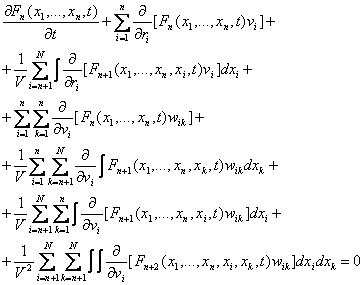(6)

Заметим теперь, что в этом уравнении третье, шестое и седьмое слагаемые тождественно равны нулю. Действительно, каждое из этих слагаемых представляет собой интеграл от трехмерной дивергенции: третье слагаемое — в пространстве координат молекулы i, шестое и седьмое —в пространстве скоростей молекулы i. По теореме Гаусса они могут быть преобразованы в интеграл по граничной поверхности. Но функция Fn обращается в нуль, когда координаты любой частицы газа соответствуют точкам, лежащим на абсолютно непроницаемой стенке сосуда и, с другой стороны, функция распределения Fn стремится к нулю, когда . Поэтому интеграл от дивергенции равен нулю и в координатном пространстве, и в пространстве скоростей. С другой стороны, пятое слагаемое в (6) можно преобразовать следующим образом. Отдельные слагаемые суммы по k отличаются лишь обозначением переменной интегрирования

Таким образом, получаем окончательно систему уравнений

. (7)

Эта система в зарубежной литературе называется обычно ББКГИ-системой (Борн, Боголюбов, Кирквуд, Грин, Ивон). Мы будем в дальнейшем для краткости, а также потому, что Боголюбову принадлежит наиболее детальный ее анализ, называть ее системой уравнений Боголюбова. в формуле (7) есть оператор Лиувилля для подсистемы из п частиц. Система уравнений Боголюбова является «зацепляющейся», так как уравнения для функции Fn содержат в правой части функцию Fn+1. Физически это отражает факт незамкнутости любой группы из n молекул (n<N), взаимодействующих с остальными N — n молекулами. Оператор Лиувилля, как видно из (7), однозначно определяет временную эволюцию функции Fn(х1, ., хп, t) для замкнутой системы частиц, в то время как правая часть (7) описывает ее незамкнутость.

Заметим, что последнее уравнение системы (7) для функции Fn является замкнутым и тождественным уравнению Лиувилля (2). С математической точки зрения интегрирование системы уравнений (7) следовало бы начинать с интегрирования этого уравнения. При этом, естественно, не нужно было бы интегрировать остальные N — 1 уравнения системы, так как все n-частичные функции распределения могут быть найдены по формулам (4), после того как найдена функция FN(x1, ., xN, t), и система вообще стала бы не нужной. Однако, как мы уже говорили, интегрирование уравнения Лиувилля представляет собой невыполнимую практически задачу.

Таким образом, физически разумный метод решения системы уравнений Боголюбова заключается в том, чтобы начинать эту процедуру не с последнего уравнения для функции FN, а с первого для функции F1 и пытаться тем или иным способом «оборвать» эту систему. Если оказывается возможным выразить некоторую функцию Fn+1 как функционал от функций Fl (ln), то такой «обрыв» системы (7) становится возможным, и мы придем к системе с конечным числом уравнений. В частности, если удается тем или иным способом выразить как функционал от F1 (x1, t) функцию F2 (х1, х2, t), мы получаем уравнение для одночастичной функции F1 (xl, t), которую принято называть кинетическим уравнением. Уравнение Больцмана и уравнение Фоккера-Планка представляют собой частные случаи кинетических уравнений.

Мы уделяем особое внимание одночастичной и двухчастичной функциям F1 (xl, t) и F2 (xl, x2, t) по следующим причинам. Через одночастичную функцию могут быть выражены важные для газодинамического описания величины: средняя плотность числа частиц n(r, t), средняя скорость потока частиц и(r, t), средняя кинетическая энергия 3/2T(r, t), которые определяются формулами

(8)

(9)

(10)

И другие важные для газодинамики величины, такие как тензор вязких сил, поток тепла и т. д., выражаются через одночастичные функции распределения. Двухчастичная функция распределения имеет особо важное значение для равновесного состояния системы. В равновесном состоянии она описывает корреляции между положениями частиц, имеющие, важное значение в теории флуктуации и в теории фазовых переходов.

Заметим, наконец, что в определение n-частичных функций Fn(x1, ., хN, t), так же как и в определение FiN) (х1, ., xN, t), вероятностный смысл был нами вложен «насильственно», и мы по существу получили систему уравнений (7), полностью эквивалентную уравнению Лиувилля, совершенно не связывая функции Fn с вероятностными характеристиками единичной системы. Отсюда следует, что система уравнений (7) есть система механических, а не статистических уравнений. Неудивительно поэтому, что эта система, так же как и уравнение Лиувилля, инвариантна по отношению к отражению времени — замене и не может описывать необратимые макроскопические процессы. Необратимость вносится в формализм теории только определенными гипотезами сугубо вероятностного характера. Запишем в явном виде уравнения для F1 и F2, которыми нам придется заниматься более детально; при этом мы отбросим в множителе (N — n)/V, входящем в (7) слагаемое n=1, 2: