Уравнения Больцмана, Лиувилля, Боголюбова

Рассмотрим некоторые приближенные методы интегрирования системы уравнений Боголюбова. Эти методы основаны на том, что в двух случаях - весьма разреженного газа и при слабом взаимодействии между частицами газа - влияние одной частицы на состояние других частиц должно становиться слабым, и можно сделать пробное допущение о том, что в нулевом приближении n-частичная функция распределения факторизу

ется, т. е. представляется в виде произведения одночастичных функций

. (15)

Отклонение точной n-частичной функции от факторизованного нулевого приближения принято характеризовать с помощью так называемых корреляционных функций Gn (x1, ., хп, t), которые находятся по следующей схеме.

Для двухчастичной функции имеем

F2(0) (х1, х2, t) = F1 (х1, t) F1 (х2, t), (16)

F2 (x1, x2, t) = F2(0) (x1, x2, t) + G2 (x1, x2, t). (17)

Для трехчастичной функции -

F3(0) (х1, х2,x3, t) = F1 (х1, t) F1 (х2, t) F1 (х3, t), (18)

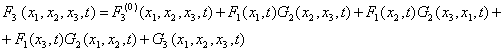(19)

и т. д.

Сформулируем теперь количественно условие разреженности газа и условие слабости взаимодействия. Пусть r0 — радиус действия межмолекулярных сил и U0 — характерная величина потенциальной энергии взаимодействия. Случай разреженного газа осуществляется, если r0 много меньше среднего расстояния между частицами ω1/3, и, следовательно, в этом случае малым параметром задачи является величина . Случай слабого взаимодействия реализуется, если потенциальная энергия мала по сравнению с кинетической энергией ~ Т. Следовательно, в этом случае малым параметром задачи является величина β= U0/T.

Допустим, что в обоих случаях корреляции между координатами и скоростями частиц являются слабыми и корреляционные функции Gn (x1, ., хп, t) малыми по параметрам а или β соответственно.

Для того чтобы построить методы решения системы уравнений Боголюбова в этих предположениях, запишем систему (7) в более детализированном виде

(20)

выделив в операторе слагаемые, содержащие и не содержащие потенциал взаимодействия

(21)

(22)

(23)

Перейдем в уравнениях (20) безразмерным переменным, выбрав в качестве единицы длины r0, скорости , ускорения и времени . Для простоты мы не будем вводить новые обозначения для безразмерных переменных и сделаем в уравнениях (20) замены

,

(24)

Кроме того, учитывая условие нормировки (19) для функци Fn(x1, ., хN, t), из которого видно, что Fn имеет размерность , введем безразмерную функцию распределения с помощью замены

(25)

Тогда уравнения Боголюбова (20) при запишутся в виде

(26)

Заметим, что, предполагая факторизацию функций Fn в нулевом приближении,

Fn(0) = F1 (х1, t) F1 (х2, t)…F1(xn,t), мы получим для одной и той же функции F1 (xi, t) N уравнений. Ясно, что необходимым условием допустимости факторизации является совместность этих уравнений нулевого приближения.

Убедимся, что случай разреженного газа () приводит в нулевом приближении к несамосогласованной системе. Действительно, система уравнений (26) в нулевом приближении выглядит следующим образом:

Легко видеть, что уравнения этой системы будут совместными только при условии отсутствия взаимодействия между частицами wik = 0. Следовательно, в случае разреженного газа корреляциями нельзя пренебрегать даже в нулевом приближении. Собственно говоря, этого следовало ожидать, так как для разреженного газа а << 1 «хорошим» кинетическим уравнением является уравнение Больцмана, которое несовместимо с требованием факторизации. Мы видели, что вывод уравнения Больцмана по Боголюбову предполагает только факторизацию функции F2 в «бесконечном прошлом».

Рассмотрим случай β = U0/T <<; 1, , что соответствует горячему газу со слабым взаимодействием между частицами, который, однако, может быть достаточно плотным. Фактически при типичной глубине потенциальной ямы U0~ (10-1 - 10-2) эв U0/T<<1 выполняется уже при комнатных температурах. В этом случае в нулевом приближении получаем незацепляющиеся уравнения

(27)

в которых переменные х1, ., хп разделяются. Это значит, что предположение является самосогласованным и одночастичная функция F1(0)(r, v, t) подчиняется уравнению

(28)

Интегрируя уравнение характеристик

(29)

находим, что решение уравнения (28) имеет вид

(30)

где ψ(r,v,t) - произвольная функция своих аргументов, совместимая с начальными и граничными условиями. Из выражения (30) следует, что F1(0)(r, v, t) остается постоянной вдоль динамической траектории частиц в μ-пространстве, чего и следовало ожидать для системы слабо взаимодействующих частиц в нулевом приближении.

Следующие приближения для функций Fn могут быть найдены последовательно из уравнений:

(31)

Решая первое из этих уравнений, можно в принципе найти F1, решая затем второе уравнение — найти G2 и, следовательно, F2 и т. д.

Мы ограничимся нулевым приближением (30) и в качестве иллюстрирующего примера рассмотрим задачу о свободном расширении газа в пустоту. Пусть в начальный момент t = 0 газ с максвелловским распределением по скоростям в одномерном случае занимает полупространство х<0. Затем стенка х = 0 удаляется и газ начинает расширяться.

 Скачать реферат