Исследование сопротивления вертикальным нагрузкам бипирамидальных свай

Рис. 2.12. Схема к интегрированию решения Миндлина

матрицы (КВВ)

Последний вариант взаимодействия частей фундамента, когда источники находятся на нижнем конце фундамента, а точка наблюдения так же находится на нижнем конце фундамента.

Для вычисления коэффициентов влияния загружения элементов нижнего конца (j=1,NE2) на точки наблюдения, находящиеся посере

дине элементов нижнего конца, вычисляется двойной интервал (2.13)

где

Если учитываются вертикальные перемещения грунта примыкающего к поверхности фундамента, только от действия вертикальных сил, приложенных на боковой поверхности (KSS, KSB) и на нижнем конце (KBS, KBB), то глобальная матрица К имеет вид (2.14)

Система алгебраических уравнений для определения неизвестных напряжений на боковой поверхности и под нижним концом записывается следующим образом (2.15)

где fsb - неизвестные напряжения на поверхности фундамента;

wed - вектор-столбец единичных перемещений узлов поверхности фундамента. В случае, если принять сваю абсолютно жесткой (т. е. несжимаемой), то перемещения всех узлов будут одинаковыми. В данной работе компоненты вектора-столбца wed принимались равными осадке фундамента при которой график зависимости "нагрузки-осадки" имеет прямолинейный вид. Как показывает анализ опытных данных для призматических свай такая осадка равна 0,01 м, для пирамидальных и фундаментов в вытрамбованном котловане - 0,015 0,020 м.

Если учитывать, что на боковую поверхность фундамента действуют радиальные напряжения s2, то глобальная матрица [K] будет содержать девять подматриц и уравнение равновесия (2.15) примет вид: (2.16)

где KRS - матрица, которая содержит коэффициенты влияния на вертикальные перемещения узлов боковой поверхности фундамента, при загружении элементов боковой поверхности радиальными напряжениями s2 (sigm2);

KSU - матрица, коэффициенты которой отражают связь между горизонтальными перемещениями узлов боковой поверхности фундамента, когда боковая поверхность загружена вертикальными напряжениями;

KRU - матрица содержащая коэффициенты влияния, которые отражают зависимость между горизонтальными перемещениями узлов боковой поверхности фундамента при загружении элементов боковой поверхности горизонтального напряжения s2;

KBU - матрица, коэффициенты которой отражают зависимость горизонтальных перемещений узлов боковой поверхности фундамента при загружении элементов нижнего конца вертикальными напряжениями s1;

KRB - матрица, коэффициенты которой отражают связь между вертикальными перемещениями узлов нижнего конца фундамента при загружении элементов боковой поверхности радиальными напряжениями s2.

{fsb} - вектор-столбец, содержащий неизвестные: касательные напряжения на боковой поверхности фундамента t, горизонтальные напряжения на боковой поверхности фундамента s2 и вертикальные напряжения на нижнем конце фундамента s1;

- вектор-столбец, содержащий заданные вертикальные перемещения узлов боковой поверхности фундамента ed1; горизонтальные перемещения узлов боковой поверхности ed2 (если свая не сжимается ed2=0); вертикальные перемещения узлов нижнего конца фундамента ed3.

Фундаментальное решение Миндлина в матрицах KRS и KRB имеет следующее выражение:

(2.17)

где (2.19)

(2.20)

x = r×cosq - arc; (2.21)

y = -r×sinq. (2.22)

Коэффициенты матрицы KRS вычисляются с использованием фундаментального решения Миндлина KW3 и интегрирования выражения

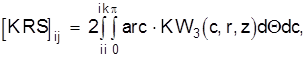(2.23)

где r = arz. (2.24)

Коэффициенты матрицы KRB вычисляются с использованием фундаментального решения Миндлина KW3 и интегрирования выражения (2.25)

где (2.26)

При вычислении коэффициентов матриц KSU и KBU используется решение Миндлина (2.27)

где R1, R2, r1 - определяются по формулам (2.4), (2.5), (2.6).

Коэффициенты матрицы KSU вычисляются интегрированием выражения (2.28)

где (2.29)

Коэффициенты матрицы KBU равны интегралу (2.30)

где (2.31)

Фундаментальное решение Миндлина в матрице KRU определяется формулой

(2.32)

где R1, R2, x, y - определяются по формулам (2.19), (2.20), (2.21), (2.22).

Коэффициенты матрицы KRU определяются интегралом (2.33)

где r = arz. (2.34)

2.2.4. Определение напряжений на поверхности фундамента

Когда сформирована глобальная матрица К и задан вектор-столбец

(2.35) решается система алгебраических уравнений (2.16) методом Гаусса с помощью процедуры GAUSP, в результате получим значения напряжений t и s2 в узлах боковой поверхности и напряжение s1 в узлах нижнего конца фундамента.

2.2.5. Определение общего сопротивления фундамента

Усилия на элементах боковой поверхности фундамента получим (2.36)

а усилия на элементах нижнего конца (2.37)

Суммарное значение силы трения определяется (2.38)

а сила под нижним концом (2.39)

Общее сопротивление фундамента при заданной осадке r = ed1 равно

Рс = Рб + Р0; (2.40)

Таким образом в результате применения изложенной методики расчета по методу граничных элементов с использованием решения Миндлина можно определить общее сопротивление фундамента в вытрамбованном котловане при заданной осадке.

Раздел 3. Результаты теоретических исследований сопротивления бипирамидальных свай

В данной работе согласно, описанной в разделе 2 методике, выполнены расчеты сопротивления бипирамидальных свай для грунтовых условий и типоразмеров свай по результатам исследований, представленных в работах [10 ¸ 15]. Теоретические модели взаимодействия свай в этих работах построены на основе теории проф. Голубкова В.Н. с использованием понятий зон уплотнения и деформаций. Эта теория построена на применении опытных данных, имеет полуэмпирический характер и требует дальнейшего развития.

 Скачать реферат