Тепломассообмен при испарении и горении капель жидких топлив

Гораздо меньше работ посвящено исследованию горения углеводо-родных топлив во влажном окислителе. Разработана числовая модель для изучения переходного состояния процессов физического испарения капли, воспламенения и диффузионного горения. Считается, что капля состоит из водного ядра, окружённого жидкой топливной оболочкой. На стадиях физического испарения и диффузионного горения возможно рассмо

трение квазистационарного процесса. На стадии диффузионного горения рассмотрены случаи, когда температура водного ядра превышает температуру кипения до тех пор, пока полностью не испарится топливо.

Изучено воздействие водяного пара на температуру пламени, скорость сгорания. Установлено, что введение водяного пара приводит к некоторому снижению температуры пламени и скорости сгорания топлив. Введение водяного пара приводит к значительному ингибированию образования C и CO при одновременном повышении тепловыделения, что связано с тем, что подача воды увеличивает концентрацию OH-радикалов, которые реагируют с CO и C, образуя CO2 и H2.

Изучен процесс сгорания тяжёлого нефтяного топлива с использованием впрыска в камеру сгорания водного пара. В зависимости от температуры и характера насыщения смеси водяным паром, определяющих соотношения влаги и воздуха в смеси, подаваемой в зону горения, рассмотрены 3 типа сгорания топлива: нормальное влажное, неполное влажное и переувлажнённое. Подчёркнуто, что для обеспечения максимальной эффективности от впрыска воды необходимо правильно устанавливать соотношение между водой и воздухом в смеси, поскольку от него зависит количество воздуха, необходимого для полного выжигания пористых коксовых остатков у зоны горения.

Как видно из обзора литературы, экспериментаторы в основном исследовали влияние воды на характеристики горения, непосредственно смешивая топливо с водой. Но существует и другой способ введения воды в зону химической реакции – горение топлива во влажном окислителе. Для построения модели горения совокупности капель в камере сгорания, необходимо горение одиночной капли.

Раздел 2

Критическое условие воспламенения капли.

2.1 Метод Зельдовича

Для вывода критического воспламенения воспользуемся методом Зельдовича Я.Б. Разделим область rк < r < rпл на две зоны: первая прилегает к поверхности приведенной пленки rв < r < rпл; вторая - rк < r < rв. Здесь rв - координата условной границы, на которой происходит воспламенение. Пренебрегая теплом, выделяющимся при химической реакции во второй зоне rк < r < rв, уравнение (1.2) запишем в виде

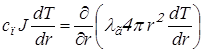(2.1)

решая которое получим

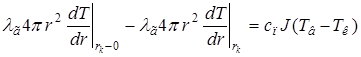
а с учётом

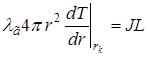
имеем выражение для теплового потока

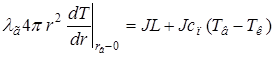(2.2)

Для первой зоны rв < r < rпл, пренебрегая изменением температуры с координатой , так как действие химических источников способствует выравниванию температуры по зоне, получим

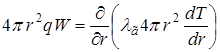(2.3)

Сравнивая (2.1) и (2.3) видим, что на границе двух зон r = rв должна существовать область ,в которой

(2.4)

т.е. количество тепла, выделяемое за счёт химической реакции , равно теплу, отводимому . Равенство (2.4) представим в виде первого условия Семёнова

Второе условие Семёнова, определяет неустойчивость теплового равновесия

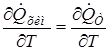(2.5)

Подставив в (2.4) из (2.2)

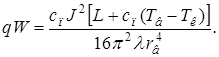(2.6)

Скорость химической реакции зависит от концентрации паров и температуры. Для определения связи концентрации с температурой запишем уравнение диффузии

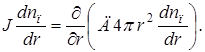
Учитывая подобие граничных условий для температуры и концентрации, можно доказать, что

.

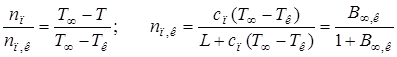Скорость химической реакции в случае избытка окислителя определяется кинетическим уравнением первого порядка

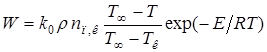(2.7)

и зависит только от температуры.

Используя уравнения Семёнова, (2.4) и (2.5), имеем систему уравнений

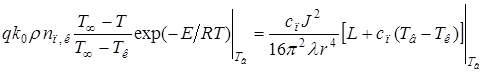(2.8)

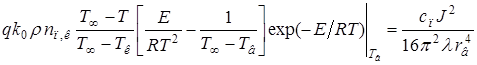(2.9)

из которой надо исключить температуру парогазовой смеси Тв.

Разделив (2.8) на (2.9), получим уравнение

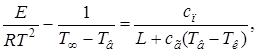
позволяющее выразить Тв через температуру среды. Оценка величины даёт малую величину по сравнению с . Поэтому без особой погрешности примем

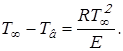(2.10)

Из (1.13) имеем ранее полученную формулу для массовой скорости испарения

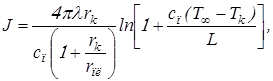(2.11)

которая при Nu = 2

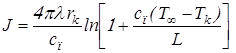. (2.12)

Выполним преобразование Франк-Каменецкого

Подставим в (2.8) и используем (2.10)

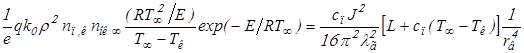
Найдём радиус воспламенения, интегрируя уравнение (2.2) в пределах от rк до rв и от rк до rпл. В результате получим

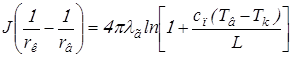
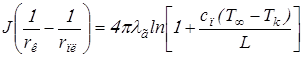
Используя формулу (2.11), имеем

,

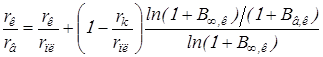где

Учитывая (2.10) и представляя

 Скачать реферат