Основы физики атмосферы

если насыщенный пар подчиняется ур-нию состояния идеального газа , то

при испарении ; , при возгонке ;.

В интегральном виде width=178 height=50 src="images/referats/13427/image023.png">

Термодинамические процессы в атмосфере

В атмосфере происходят различные термодинамические процессы, в частности, изотермические, адиабатические и другие знакомые по курсу молекулярной физики процессы. В основном атмосфера неизотермична, например, в тропосфере температура меняется с высотой довольно сильно, примерно на 6,5 °С на км. Но в областях тропопаузы, стратопаузы, мезопаузы в некоторых диапазонах высот ее приближенно можно считать изотермичной.

Как известно, распределение давления и плотности в изотермической атмосфере определяется формулой Больцмана. Разность давлений в слоистой и статичной атмосфере обусловлена весом выделенного объема воздуха:

Ось z направлена вверх. Если заменить р выражением, получен­ным из уравнения состояния (13.2), то получим уравнение

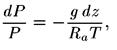
откуда после интегрирования следует формула Больцмана

где — так называемая высота однородной атмосферы.

В соответствии с формулой Больцмана давление с высотой меняется экспоненциально, причем Н определяет масштаб спадания давления по высоте, т. е. на высоте Н давление падает в е раз. Формула для плотности будет аналогичной, потому что при постоянной температуре плотность пропорциональна давлению. Высоту однородной атмосферы можно выразить и через массу т одной молекулы:

Численная оценка дает величину около 8 км:

Заметим, что уже на высотах в несколько километров спадание давления и плотности воздуха значительно, например, на высоте 2,5 км плотность составляет 70% от плотности на уровне моря. Однако, как правило, в атмосфере происходят заметные изменения температуры с увеличением высоты, и приближение

изотермической атмосферы явно неприменимо. Более подходя­щим приближением при рассмотрении перемещения частиц воздуха является адиабатическое приближение. При таком анализе обычно выделяется малая частица, представляющая собой «физически бесконечно малый» объем, но достаточно большая, в том смысле, что она содержит много молекул. Иными словами, предполагается, что частица достаточно велика по сравнению с масштабами микроструктуры среды и достаточно мала по сравнению с внешними характерными масштабами задачи. Поскольку воздух — плохой проводник тепла и его теплопроводность низка, можно считать, что по мере перемещения этой частицы с потоком других частиц, с ветром, она слабо обменивается энергией с окружающей средой, т.е. можно использовать адиабатическое приближение. Такая простейшая модель, тем не менее, отражает основное физическое явление и объясняет многие процессы в атмосфере.

Рассмотрим адиабатический процесс в атмосфере. Первое начало термодинамики имеет вид

Здесь приращение тепла δQ равно приращению внутренней энергии dU = CVdT плюс работа ЗА = P dV. Отметим, что в об­щем случае только приращение внутренней энергии dU является полным дифференциалом. Для частицы, которая будет переме­щаться, не меняя своей энергии, можно написать δQ = О, т.е. приток тепла равен нулю, взаимодействие с окружающей средой отсутствует или, по крайней мере, пренебрежимо мало за время этого перемещения. Если мы хотим получить зависимость Р(Т), надо перейти от дифференциала dV к дифференциалу dP. Это несложно сделать, используя уравнение состояния идеального газа. Дифференцируя логарифм соотношения (13.1), получим

После интегрирования получается связь

Это так называемое тождество Майера. Далее, используя тождество Майера, заменяем дифференциал dV на dP в (13.5) и получаем

уравнение адиабатического процесса:

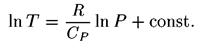
Отсюда отношение температур равно отношению давлений в степени R/Cp. Универсальная газовая постоянная равна, как известно, разности теплоемкостей

Тогда, заменяя R на разность Ср — Сv, получим для адиабатического процесса формулу

в которой отношение температур есть отношение давлений в степени 1 — 1/y где y = Ср/Сv . Воздух при нормальных условиях состоит в основном из молекул N2 и О2. У таких двухатомных молекул при типичных атмосферных температурах колебательные степени свободы не возбуждаются, поэтому они имеют 5 степеней свободы и молярную теплоемкость при постоянном объеме Су = 5/2 R, а молярную теплоемкость при постоянном давлении Ср = 7/2 R, тогда y = 7/5.

При адиабатическом подъеме, естественно, будет происходить охлаждение частиц воздуха. Давление в частице меняется так же, как и давление внешней среды. Частица — это условный элемент объема, в котором достаточно много молекул, и по мере перемещения воздуха давление в частице все время равно давлению среды. Но по мере подъема будет происходить изменение температуры частицы, и этот градиент температуры, полученный в адиабатическом приближении, называют адиабатическим градиентом температуры. Уравнение адиабатического процесса (13.6) связывает, заменяя приращение давления через гидростатическое равенство (13.4), получим уравнение для температуры при таком адиабатическом подъеме:

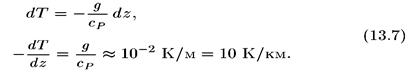
Адиабатический градиент температуры по высоте отрицателен и представляет собой отношение ускорения свободного падения g к удельной теплоемкости воздуха при постоянном

давлении.

Полученное численное значение градиента больше, чем в реальной атмосфере ( ≈ 6-6,5 К). Завышение величины температурного градиента связано с точностью адиабатического приближения, но, главное, здесь не учтено, что при конденсации водяного пара будет выделяться тепло и поднимающаяся частица будет охлаждаться слабее, т. е. рассмотренное здесь охлаждение сильнее, чем в реальной атмосфере.

 Скачать реферат