Определение реакции опор твёрдого тела

Подставляя (5) и (6) в (1), получим

(7)

Выразим из второго уравнения системы (7) величину нормальной реакции и подставим ее в первое уравнение. В результате получим

при ; (8)

=53 height=24 src="images/referats/13430/image151.png">при . (9)

где

Рассмотрим промежуток времени , в течении которого тело 1 движется вправо . Из (8) следует, что

,

где С- постоянная интегрирования, определяемая из начального условия: при

.

При скорость тела 1 обращается в ноль, поэтому .

Найдем значения и :

Т.е. , . Значит, тело при начинает двигаться в обратном направлении. Это движение описывается дифференциальным уравнением (9) при начальном условии: ; (10)

Интегрируя (9) с учетом (10), получим, при

(11)

При получим из (11) искомое значение скорости тела 1 в момент, когда

.

Точное решение задачи. Воспользовавшись методикой, изложенной выше, получим дифференциальное уравнение движения тела 1:

при (12)

; при , (13)

где

Из (12) и учитывая, что получаем, при

откуда 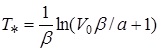или

Из (13) и учитывая, что получаем, при

При находим

Ответ:.

 Скачать реферат