Методика прогноза лесной пожарной опасности

Здесь Pij – вероятность возникновения лесного пожара для j-го интервала (шага по времени) на i-й контролируемой лесной территории; Pi(А) – вероятность антропогенной нагрузки; Pi(ЛП/А) – вероятность возникновения пожара вследствие антропогенной нагрузки на площади Fi; Pi(М) – вероятность возникновения сухих гроз на площади Fi; Pi(ЛП/М) – вероятность возникновения лесного пожара от молнии при усл

овии, что сухие грозы могут иметь место на площади Fi; Pij(C) – вероятность того, что влагосодержание слоя РГМ будет меньше критического (вероятность возникновения пожара по метеоусловиям).

При выводе формулы (4) было сделано допущение о том, что лесопожарное созревание на каждом выделе контролируемой лесной территории проходит независимо друг от друга и определяется только параметрами, характеризующими данный выдел.

Здесь n – это эмпирический показатель степени, характеризующий количественное изменение пожарной опасности.

Величины Pi(А), Pi(ЛП/А), Pi(М), Pi(ЛП/М) можно найти, используя известное определение вероятности события через соответствующие частоты (статистическая модель риска)

Здесь NАi и NПАi – количество дней пожароопасных сезонов для i-го выдела, когда имеется антропогенная нагрузка, достаточная для зажигания РГМ и количество пожаров вследствие этой нагрузки, включая и умышленные поджоги за период с 2000 по 2004 год; NКПi – общее количество пожаров для i-го выдела за пять лет с 2000 по 2004 год; NМi и NПСi – число дней для i-го выдела, когда имели место молнии (при сухих грозах) и общее число дней пожароопасных сезонов для i-го выдела за период с 2000 по 2004 год; NПМi – количество пожаров от молний при сухих грозах за пять лет с 2000 по 2004 год.

1.2. Упрощенная математическая модель низкотемпературной сушки слоя растительных горючих материалов

Как уже было сказано раннее, немаловажным фактором при составлении прогноза лесной пожарной опасности является учет влагосодержания в напочвенном покрове. В предложенной детерминировано-вероятностной методике этот фактор не остался без внимания.

Далее воспользуемся формулами перехода от влагосодержания к объемным долям

Здесь ц1(k) – объемная доля сухого органического вещества k-го ОПГ, ц2(k) – объемная доля свободной и связанной воды k-го ОПГ.

Базой данных для этой модели должны служить данные о составе РГМ в напочвенном покрове и о термокинетических постоянных, характеризующих динамику сушки каждого из РГМ и РГМ, поддерживающих горение.

Зная текущее значение ц2(k) и критическое влагосодержание можно определить текущее влагосодержание и в результате вероятность возникновения лесного пожара для прогнозируемого промежутка времени.

С точки зрения физики задача о сушке слоя РГМ ставится следующим образом: известны тип растительности и проводники горения в слое РГМ, известен запас РГМ, его высота и влагосодержание, известны метеоусловия, требуется определить изменение объемной доли воды в РГМ в разные моменты времени.

Для получения упрощенной математической модели используем данную постановку задачи со следующими допущениями:

1) Конвективный теплообмен между слоем РГМ и приземным слоем атмосферы удовлетворительно описывается с помощью граничных условий третьего рода с использованием известных коэффициентов конвективного теплообмена. 2) Давление Р, температура Т и плотность r газовой фазы в слое РГМ совпадают с соответствующими метеорологическими данными (Ре, Те и rе) для данного момента времени и данной местности.

3) Излучение в слое РГМ подчиняется закону Бугера-Ламберта. 4) Испарение связанной воды и капелек воды, прилипших к элементам РГМ, описывается одним и тем же законом Герца-Кнудсена.

5) Метеорологические данные и начальные влагосодержания типичных ОПГ на территории лесхоза одинаковы для всех типичных выделов.

6) Напочвенный покров всех типичных выделов лесхоза можно разбить на пять типов: опад хвои, мох, лишайник, опад листвы, травяная ветошь.

7) Для каждого типичного выдела температура и объемная доля воды в ОПГ описывается одной системой уравнений.

В результате для математического описания сушки основного проводника горения имеем следующую систему уравнений:

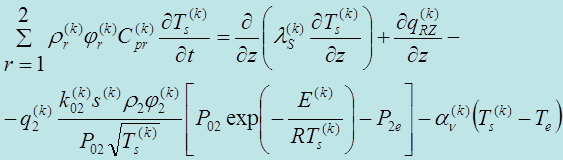
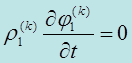
которую необходимо решать с учетом следующих начальных и граничных условий

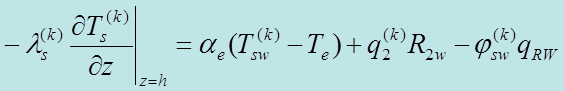
Член в левой части (8) характеризует изменение тепловой энергии в слое РГМ в единице объема за единицу времени. Первый и второй член в правой части (8) отвечают за приток тепла за счет теплопроводности и солнечного излучения. Третий член характеризует влияние влажности воздуха на сушку слоя РГМ. Четвертый член характеризует теплообмен между к-й фазой и газовой фазой в слое РГМ. Член в квадратных скобках правой части уравнения [10] характеризует влияние влажности воздуха на баланс влаги в слое РГМ. Оставшиеся параметры в правой части характеризуют скорость сушки РГМ.

Приведем систему уравнений (8), (10) к безразмерному виду

Уравнение (14) представляет собой баланс энергии в к-й фазе слоя РГМ, а уравнение (15) характеризует баланс влаги в слое РГМ, где черта сверху обозначает осреднение по высоте слоя РГМ.

Эту систему необходимо решать с учетом следующих начальных условий

 Скачать реферат