Разработка методики анализа результатов геодезических измерений при наблюдении за осадками и смещениями крупных инженерных сооружений спутниковыми методами

где N - радиус кривизны нормального сечения эллипсоида в плоскости первого вертикала, который равен

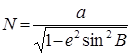, (2)

Где - большая полуось эллипсоида,

- первый эксцентриситет; (3)

Н - геодезическа

я высота.

Введем обозначение:

, (4)

геодезическая высота вычисляется по формуле

. (5)

Для того чтобы вычислить геодезическую высоту , необходимо знать широту . Для вычисления широты удобно воспользоваться формулой Боуринга:

, (6)

где .

Долгота вычисляется по формуле:

.(7)

Для перехода от геоцентрических координат к топоцентрическим координатам необходимо выбрать один пункт за исходный. При решении геодезических задач между точками в пространстве используют систему топоцентрических декартовых координат, начало координат находится в исходной точке (,,), расположенной обычно на земной поверхности. Ось расположена на продолжении нормали к поверхности эллипсоида в точке , ось расположена в плоскости меридиана точки перпендикулярно к оси и направлена в сторону оси вращения эллипсоида, ось перпендикулярна к осям и и направлена в сторону увеличения долготы.

Связь между декартовыми топоцентрическими и декартовыми геоцентрическими координатами устанавливается следующим образом:

. (8)

Чтобы найти обратные зависимости, решим эти уравнения относительно , и . В результате решения получим

; (9)

; (10)

. (11)

При использовании спутниковой навигационной системы GPS координаты земных объектов получаются в системе координат WGS-84. При выполнении геодезических работ обычно используются местные системы координат. При обработке результатов спутниковых измерений при наблюдениях за деформациями инженерных сооружений возникает необходимость отделить осадки наблюдаемых объектов от горизонтальных смещений, поэтому система координат WGS-84 не полностью отвечает поставленным задачам. В связи с этим в работе рассмотрен процесс определения средних квадратических ошибок определения топоцентрических координат.

С этой целью установим зависимость между малыми изменениями декартовых топоцентрических координат , и и геоцентрических координат начальной точки 1 и конечной точки 2.

Дифференцируем сначала равенство

.

Переменными величинами являются координаты пунктов в геоцентрической системе координат , , и , , :

(12)

Для нахождения зависимости дифференциала широты от изменений декартовых координат дифференцируем формулу Боуринга (6):

. (13)

В свою очередь

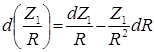. (14)

Величину определим из :

,

следовательно,

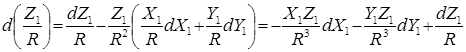. (15)

Зависимость изменения широты пункта от изменений декартовых геоцентрических координат окончательно представим в виде:

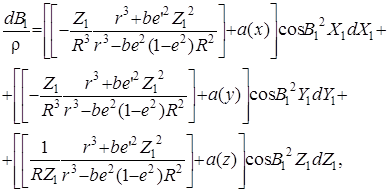(16)

где

.

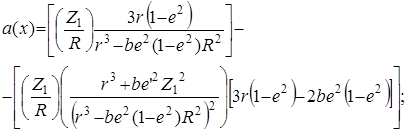
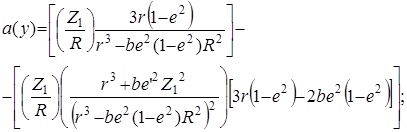
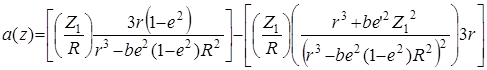Представим формулу (16) более компактно, с этой целью введем обозначения:

(17)

С учетом (17) формулу (16) представим в виде

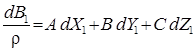. (18)

Для нахождения изменения долготы дифференцируем формулу :

. (19)

Зависимость изменения радиуса кривизна первого вертикала найдем из

,

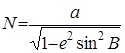следовательно

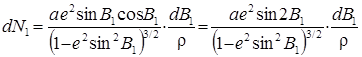. (20)

Подставив значения , и в уравнение (12), имеем

, (21)

 Скачать реферат