Система автоматического управления регулируемым электроприводом

где - коэффициент передачи механической части двигателя, а - механическая постоянная привода.

Таким образом, не учитывая нелинейности и внутренние обратные связи для упрощения вычислительных операций, можем записать передаточную функцию РЭП, которая с достаточной

точностью описывает процессы в аналоговой системе:

.

Обозначим произведение всех постоянных коэффициентов как

,

тогда

.

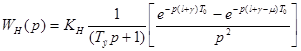Передаточная функция неизменяемой части с учетом фиксатора:

;

.

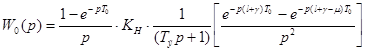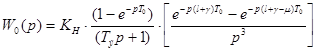Определим дискретную передаточную функцию приведенной неизменяемой части при и , учитывая, что в описании неизменяемой части имеются элементы запаздывания вида , для которых следует применять модифицированное z-преобразование [6]:

.

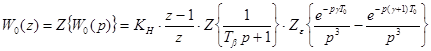Рассмотрим множители полученного выражения более детально:

1) =,

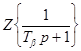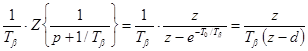где 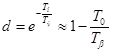, соответственно, .

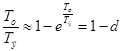2) ,

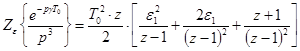где и , соответственно, .

3) ,

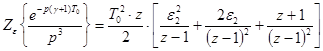где и , соответственно,

Тогда

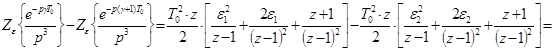
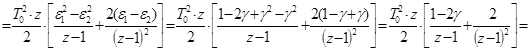
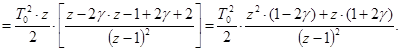
Обозначим

, ;

,

Таким образом, передаточная функция приведенной неизменяемой части:

;

.

Из анализа исходной аналоговой системы . Подставив значения получим:

;

.

4.3.2 Определение желаемой дискретной передаточной функции

Основой для синтеза регулятора скорости являются заданные статические и динамические параметры САУ электропривода, по которым определяется желаемая дискретная частотная характеристика системы . Зная частотную характеристику неизменяемой части системы , можем определить частотную характеристику регулятора как

.

Тип желаемой частотной характеристики зависит от требуемого порядка астатизма. В справочниках [7, 8] приводится несколько видов типовых ЛАЧХ, которые полностью определяются заданием четырех величин: коэффициента усиления и трех сопрягающих частот. Один из возможных вариантов желаемой характеристики приведен на рисунке 4.3.2. Описывается она следующим выражением:

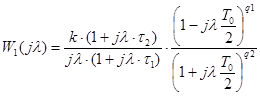
Рисунок 4.3.2 – Желаемая логарифмическая частотная характеристика

Значения параметров выбранной желаемой частотной характеристике рассчитываются следующим образом:

1) эквивалентная частота гармонического управляющего воздействия:

;

с-1;

2) коэффициент передачи разомкнутой системы

;

, с-1;

3) сопрягающая частота , для которой в низкочастотной области справедливо допущение : с-1;

4) базовая частота запретной области ЛАЧХ :

;

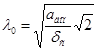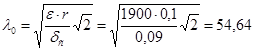с-1;

5) сопрягающую частоту определяем по показателю колебательности , приняв М=1,2:

,

с-1;

6) третья сопрягающая частота

;

с-1;

7) постоянные времени , :

; с-1;

; с-1.

Таким образом, желаемая дискретная частотная характеристика описывается следующим выражением:

.

 Скачать реферат