Зеркальные антенны

Введение

Антенна выступает в роли промежуточного звена радиоприбором – приемником или передатчиком – и окружающим пространством, являясь своего рода преобразователем электромагнитной энергии, её трансформатором. Передающая антенна, питаемая энергией радиопередатчика, возбуждает в пространстве электромагнитное поле, несущее сигнал. Незначительную часть энергии поля ула

вливает приемная антенна, создающая на входе радиоприемника эдс, достаточную для воспроизведения сигнала.

С изобретением радио начинается история антенной техники, которая проходит свои этапы вместе с развитием радиотехники. Однако элементы, излучавшие электромагнитную энергию и отбиравшие ее из пространства, были известны уже в опытах Генриха Герца (1886–1888гг.) до возникновения самой идеи об использовании электромагнитного поля для передачи сигналов. Впоследствии нашим знаменитым соотечественником А. С. Поповым была изобретена первая радиотехническая антенна.

Вслед за первыми шагами радиотехники, когда использовались искровые и дуговые генераторы, задачам радиосвязи были подчинены длинные и средние, а затем и короткие волны. За это время – к середине тридцатых годов – возникли и сформировались все основные типы проволочных антенн, или «радиосетей». Антенны длинных и средних волн по своим размерам почти всегда меньше длины волны. Освоение же коротких волн означало качественный скачок в антенной технике, так как открылась реальная возможность построения антенн, значительно превышающих длину волны и поэтому обладающих большой направленностью действия. Тенденция к дальнейшему укорочению рабочей волны ещё сильнее проявляется в последующий период, начиная с предвоенных лет. Как известно, благодаря появившимся недавно оптическим квантовым генераторам практике теперь доступны когерентные электромагнитные колебания светового диапазона, что открывает совершенно новые возможности в радиосвязи.

1. Действие зеркал

Рефлек­тором для антенны являлась такая же антенна, расположенная на расстоянии четверти волны и питаемая в опережающей квадратуре либо не присоединенная к источнику,- «пассивная» антенна. В последнем случае отражение оказывалось неполным: антенна с пассивным рефлектором обладает некоторым обратным излучением.

Рис. 1

Между тем, можно представить совершенный пассивный рефлек­тор в виде расположенной за антенной Р (рис. 1а) идеально проводящей плоскости. Если расстояние Н выбрано так, что при отражении в направлении нормали волна приходит к Р в фазе с прямым излучением, то амплитуда поля в этом направлении удваивается. В случае параллельного отражающей плоскости линей­ного вибратора (рис. 1б) ее действие эквивалентно находящему­ся на расстоянии 2h противофазному вибратору и, следова­тельно, для удвоения излучения по нормали нужно брать

Применяя рассмотренный принцип на практике, не стремятся к максимально возможному увеличению плоского пассивного рефлектора.

Достаточно (рис, 1в), чтобы края этого антенного зеркала были видны из Р под углом 2α0, внутри которого сосредоточено все или почти все обратное (270° > а > 90°) излучение антенны Р. Тогда обратное излучение антенны с зеркалом будет пренебрежимо мало.

В дальнейшем при изучении антенных зеркал будем предполагать, что все размеры системы - в том числе и расстояние облучателя от зеркала - значительно превосхо­дит длину волны, так что применимы правила геометрической оп­тики.

Рис. 2

Следя за ходом лучей, отраженных от плоского зеркала (рис.2а), легко заметить, что угловая ширина пучка лучей, па­дающего на зеркало, при отражении сохраняется. На (рис.2б) для сравнения показано кривое зеркало, поверхность которого спе­циально выбрана с тем расчетом, чтобы пучок лучей, расходящийся из Р, превратить в параллель­ный - с угловой шириной 2а0 = 0°. Такое зеркало создает синфазное поле в своем плоском раскрыве, след которого показан пунктиром на рис.б. В зависимости от характера облучающей антенны оно более или менее близко к полю в раскрыве иде­альной поверхности антенны.

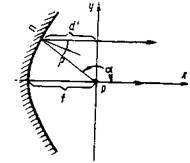Параболическое зеркало. Покажем, что изображенный на рис.3 про­филь зеркала, собирающего расходя­щийся пучок лучей в параллельный, описывается параболой. На рис. 3 сделаны построения, необходимые для этого вывода. Начало координат совмещено для удобст­ва с точечным облучателем зеркала Р.

Рис. 3

Профиль зеркала можно было бы найти из условия, что при от­ражении от его поверхности должен выполняться закон Снеллиуса: угол отражения равен углу падения. Это привело бы к дифференциальному уравнению кривой. Но проще задаться равенством всех оптических путей из начала координат до плоскости х = 0:

Рассматривая центральный луч, видим, что

Учитывая также равенства

имеем

откуда после простых преобразований получается уравнение пара­болы

где

Величина f называется фокусным расстоянием парабо­лического зеркала.

Уравнение можно записать и в полярных координатах, сделав в выражении

замену

Оно имеет вид

Рис. 4

На рис. 4 введены следующие обозначения: диаметр параболического зеркала D, глубина d и угол раскрыва 2α0; зеркало рис.4а, для которого называется длиннофокусным, а зеркало рис.4б -короткофокусным, так как для него

Внося в (5.69) координаты края зеркала находим следующее соотношение, связывающее его линейные раз­меры с фокусным расстоянием:

 Скачать реферат