Анализ случайных процессов в линейных системах радиоэлектронных следящих систем

Рис.2. Зависимость АЧХ от постоянной времени инерционного звена.

Используя (4) можно оптимизировать параметры системы, в частности по критерию минимума флюктуационной ошибки. С этой целью продифференцируем (6.4) по и приравняем производную нулю.

;

;

;

; ;

при ; ;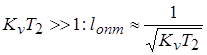

Подставив в (4), получим

,

где - собственная частота следящей системы.

Если задающее воздействие представлено спектральной плотностью неточность его воспроизведения также оценивается дисперсией. Рассмотрим пример (рис.3).

Рис.3

Пусть ; ,

где ─ дисперсия задающего воздействия;

- параметр, определяющий ширину спектра.

Определим величину дисперсии ошибки слежения , обусловленную неточностью воспроизведения задающего воздействия.

;

,

где; - коэффициент передачи интегратора;

- крутизна дискриминационной характеристики.

; ;

приведем выражение к стандартному виду:

;

(jw) =( +jw) (Kv+jw) =(jw) 2 +(+Kv) jw+ Kv;

; ;

; ; ; ;

; ;

При увеличении уменьшается, в то время как в первом примере увеличивается.

Эквивалентная шумовая полоса следящих систем

Под эквивалентной шумовой полосой следящей системы понимают полосу пропускания эквивалентной системы, имеющей прямоугольную АЧХ, одинаковое с исходной системой ее значение на нулевой частоте и одинаковую дисперсию на выходе при воздействии на входы систем белого шума (рис.4).

Рис.4. АЧХ исходной и эквивалентной систем.

Чтобы определить полосу пропускания используем условие равенства дисперсий:

Отсюда

.

Использование значения эквивалентной шумовой полосы позволяет упростить вычисление дисперсии:

; .

Если , то , или ,

где ─ односторонняя спектральная плотность.

Формулы для расчета эквивалентной шумовой полосы систем приведены в табл.1

Таблица 1. Формулы для расчета эквивалентной шумовой полосы.

Оптимизация параметров следящих систем

Для решения задачи оптимизации необходимо определить структуру системы, предъявляемые требования и ограничения, накладываемые на систему, описать воздействия и возмущения, выбрать критерий оптимизации и метод.

Оптимизируем параметры kи2 и T1 в системе (рис.5), в которой задающее воздействие λ(t) – детерминированная функция, а возмущение ─ случайный процесс ξ(t).

 Скачать реферат