Анализ системы управления

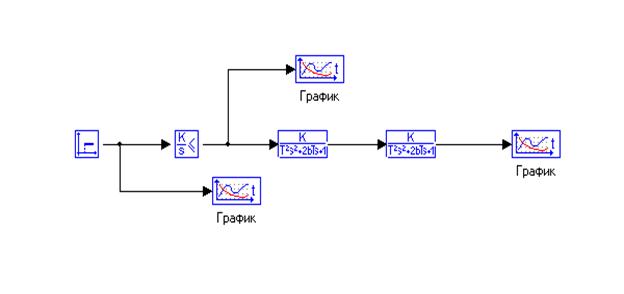
Рисунок 5.1 - Исполнительный механизм и объект управления.

График ступенчатого входного воздействия изображён на рисунке 5.2.

Рисунок 5.2 – График входного сигнала

График сигнала, преобразованного исполнительным механизмом, изображён на рисунк

е 5.3.

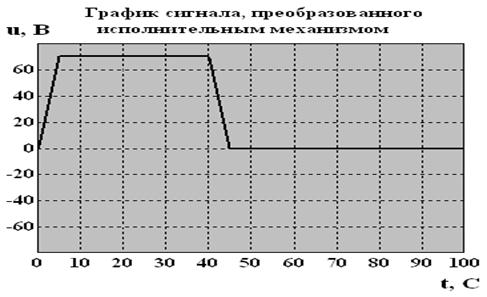
Рисунок 5.3 - График сигнала, преобразованного исполнительным механизмом

График переходного процесса, протекающего в системе управления, изображён на рисунке 5.4.

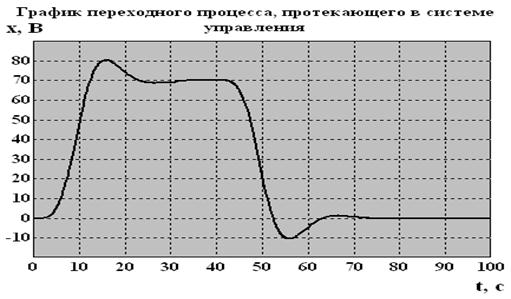
Рисунок 5.4 - График переходного процесса, протекающего в системе управления

Анализ динамических свойств последовательного соединения исполнительного механизма и объекта управления при скачкообразном изменении Up от 0 до 70 В при t=0 до -70 при t=40c проводится с помощью данных, на основании которых построен график на рисунке 5.4.

На графике можно выделить два периода. Первый – от 0 до 40 с, второй скачок начинается от 40с. Но для анализа системы достаточно проанализировать один (любой) из участков по причине того, что основные параметры периодов будут совпадать.

Проанализируем первый период:

хуст=70 B,=±3,5 B.

tн= 22,44 c. Достигается при t = хуст.

xmax = 79.39 B. Достигается при t = 18.77 c.

Высчитаем перерегулирование:

Переходной процесс системы превышает значение ошибки регулирования, значит процесс осуществляется с перерегулированием.

6. РАЗРАБОТКА РЕЛЕЙНОГО РЕГУЛЯТОРА

Для конструкции релейного регулятора используется блок «Релейная неоднозначная с зоной нечувствительности». Наглядная схема приведена на рисунке 7.

Значение параметров ступенчатого входного воздействия:

1) Время «включения» скачка t=0;

2) Значение сигнала до скачка Y0=0;

3) Значение сигнала после скачка YK=40;

Значение параметров статической характеристики реле

a1, a2, b1, b2, y1, y2 - -3.5 -3.5 3.5 3.5 -70 70;

Ниже (рисунок 6.1) приведена схема системы с включением блока реле неоднозначное с зонами нечувствительности (выполнена с помощью ПО ПК «МВТУ»).

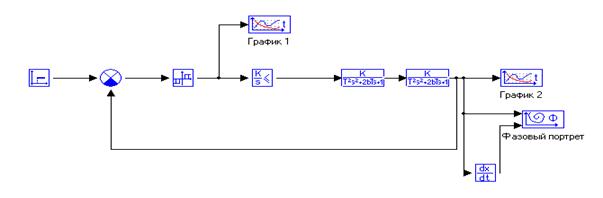
Рисунок 6.1 – Схема системы с включением блока реле

В этом случае график процесса, протекающего в системе, будет выглядеть следующим образом (рисунок 6.2):

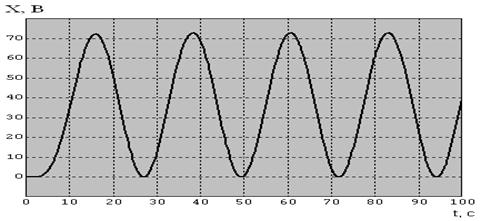
Рисунок 6.2 - График процесса, протекающего в системе при подключении реле

Фазовый портрет представлен на графике (рис. 6.3):

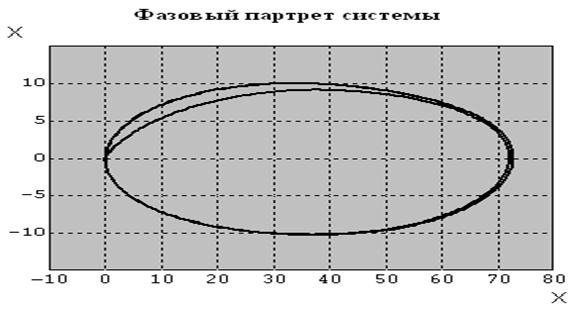
Рисунок 6.3 – Фазовый портрет процесса, протекающего в системе при подключении реле

Как следует из приведённых выше графиков, в системе возникают незатухающие колебания. Амплитуда колебаний зависит от начальных условий и, следовательно, эти колебания являются автоколебаниями. Для устранения колебаний необходимо ввести в систему обратную связь с апериодическим звеном первого порядка и сумматором. Обратная связь необходима для того, чтобы предсказать время отключения реле в момент, когда оно ещё не достигло зоны нечувствительности.

Схема линейного регулятора (выполнена в программе ПК «МВТУ») изображена на рисунке 6.4.

Рисунок 6.4 – Схема релейного регулятора

Таким образом был сконструирован релейный регулятор, обеспечивающий перевод объекта из начального состояния xн=0 в конечное состояние xк=40 В. Теперь можно приступить к оптимизации структуры и подбору численных значений.

7. ВЫБОР СТРУКТУРЫ И ПАРАМЕТРОВ

Как уже было показано, в качестве оптимальной структуры релейного регулятора может быть использована структура, обоснованная в п.6 (рис. 6.4).

Рисунок 7.1 – Схема релейного регулятора

В качестве численных значений изменяемых параметров структуры – значение коэффициентов и постоянной времени апериодического звена первого порядка. По умолчанию значение параметров:

1) Вектор коэффициентов – 1;

2) Вектор постоянных времени Т, с – 1;

При таких значениях график процесса, протекающего в системе будет выглядеть следующим образом:

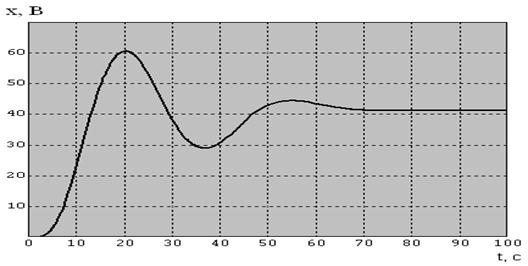
Рисунок 7.2 – График процесса, протекающего в системе

Фазовый портрет процессов представлен на рисунке 7.3

Рисунок 7.3 – Фазовый портрет процессов, протекающих в системе

На рисунке 7.2 видно ,что присутствие обратной связи с апериодическим звеном 1-го порядка выводит систему из колебательного состояния, т.е. обратная связь останавливает реле до того как оно вошло в зону чувствительности.

Рисунок 7.3 представляет собой фазовый портрет системы.

Анализ графика (рис.6.2) даёт следующие результаты:

хуст=40 B,=±3,5 B.

tн= 69.43 c. Достигается при t = хуст.

xmax = 61.1311 B. Достигается при t = 18.6964 c

%

Составим передаточную функцию замкнутой обратной связи:

Необходимо согласовать какое постоянное время необходимо поставить. Для этого решим уравнение, представленное формулой (3), из которого можно вычислить постоянное время (T).

, где (3)

y – выходной сигнал,

x – входной сигнал,

t – время за которое входной сигнал доходит до 70 В.

Так как входной сигнал равен 70В, выходной сигнал равен 40, время за которое входной сигнал доходит до 70В равно 3 секунды (время берется из рисунка 7.4)

Рисунок 7.4 – График сигнала, преобразованного звеном обратной связи.

Подставим значение в (3):

с.

Подставим в апериодическое звено постоянное время равное 1,7 секунды. Посмотрим поведения переходного процесса при таких параметрах:

1.

1) Вектор коэффициентов – 1;

2) Вектор постоянных времени Т, с – 1,7;

Рисунок 7.5 – График процесса, протекающего в системе

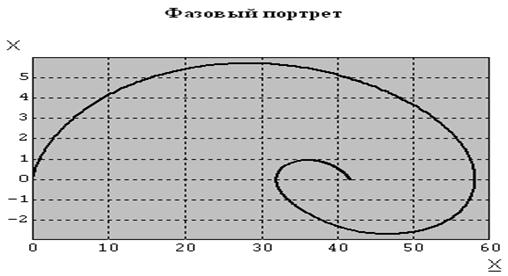
Рисунок 7.6 – Фазовый портрет процессов, протекающих в системе

В переходном режиме качество системы не удовлетворяет требованиям, следовательно, чтоб в замкнутой системе регулирования имели место плавные (без перерегулирования) и быстрые переходные процессы необходимо увеличить коэффициент усиления звена, что понизит колебательный процесс.

 Скачать реферат