Разложение функций. Теория вероятностей

Рефераты / Математика / Разложение функций. Теория вероятностей

Например.

Расстояние, которое пролетает снаряд при выстреле, есть НСВ.

ИФР называют функцию F(x), определяющую для каждого значения х вероятность того, что НСВ Х примет значение Х<х, т.е. F(x)=Р(X<x).

Часто вместо ИФР говорят ФР.

Геометрически, равенство F(x)=Р(X<x) можно растолковать: F(x) есть вероятность того, что НСВ Х примет значение, которое изображается на числов

ой оси точкой, лежащей левее точки х.

Свойства ИФ.

1. Значение ИФ принадлежит промежутку [0;1], т.е. F(x).

2. ИФ есть неубывающая функция, т.е. х2>х1,.

Следствие 1. Вероятность того, что НСВ Х примет значение, заключенное в интервале (а;в), равна приращению интегральной функции на этом интервале, т.е.

P(a<x<b)=F(b)-F(a)

Следствие 2. Вероятность того, что НСВ Х примет одно определенное значение, например, х1=0, равна 0, т.е. Р(х=х1)=0.

3. Если все возможные значения НСВ Х принадлежат (а;в), то F(x)=0 при x<а, и F(x)=1 при х>в.

Следствие 3. Справедливы следующие предельные отношения.

Дифференциальная функция распределения (ДФР) вероятностей непрерывной случайной величины (НСВ) (плотность вероятности).

ДФ f(x) распределения вероятностей НСВ называют первую производную от ИФР:

f(x)=F’(x)

Часто вместо ФДР говорят плотность вероятности (ПВ).

Из определения следует, что, зная ИФ F(x) можно найти ДФ f(x). Но выполняется и обратное преобразование: зная ДФ f(x), можно найти ИФ F(x).

;

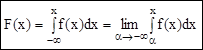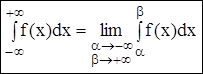
Вероятность того, НСВ Х примет значение, принадлежащее (а;в), находится:

А). Если задана ИФ – следствие 1.

Б). Если задана ДФ

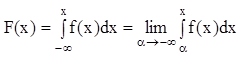
Свойства ДФ.

1. ДФ – не отрицательная, т.е. .

2. несобственный интеграл от ДФ в пределах (), равен 1, т.е. .

Следствие 1. Если все возможные значения НСВ Х принадлежат (а;в), то .

Примеры. №263, 265, 266, 268, 1111, 272, д/з.

Числовые характеристики НСВ.

1. Математическое ожидание (МО) НСВ Х, возможные значения которой принадлежат всей оси ОХ, определяется по формуле:

Если все возможные значения НСВ Х принадлежат (а;в), то МО определяется по формуле:

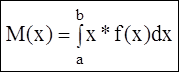
Все свойства МО, указанные для дискретных величин, сохраняются и для непрерывных величин.

2. Дисперсия НСВ Х, возможные значения которой принадлежат всей оси ОХ, определяется по формуле:

Если все возможные значения НСВ Х принадлежат (а;в), то дисперсия определяется по формуле:

Все свойства дисперсии, указанные для дискретных величин, сохраняются и для непрерывных величин.

3. Среднее квадратичное отклонение НСВ Х определяется также, как и для дискретных величин:

Примеры. №276, 279, Х, д/з.

Операционные исчисления (ОИ).

ОИ представляет собой метод, позволяющий свести операции дифференцирования и интегрирования функций к более простым действиям: умножение и деление на аргумент так называемых изображений этих функций.

Использование ОИ облегчает решение многих задач. В частности, задач интегрирования ЛДУ с постоянными коэффициентами и систем таких уравнений, сводя их к линейным алгебраическим.

Оригиналы и изображения. Преобразования Лапласа.

f(t)-оригинал; F(p)-изображение.

Переход f(t)F(p) называется преобразование Лапласа.

Преобразование по Лапласу функции f(t) называется F(p), зависящая от комплексной переменной и определяемая формулой:

Этот интеграл называется интеграл Лапласа. Для сходимости этого несобственного интеграла достаточно предположить, что в промежутке f(t) кусочно непрерывна и при некоторых постоянных М>0 и удовлетворяет неравенству

Функция f(t), обладающая такими свойствами, называется оригиналом, а переход от оригинала к его изображению, называется преобразованием Лапласа.

Свойства преобразования Лапласа.

Непосредственное определение изображений по формуле (2) обычно затруднено и может быть существенно облегчено использованием свойств преобразования Лапласа.

Пусть F(p) и G(p) являются изображениями оригиналов f(t) и g(t) соответственно. Тогда имеют место следующие свойства-соотношения:

1. С*f(t)С*F(p), С=const -свойство однородности.

2. f(t)+g(t)F(p)+G(p) –свойство аддитивности.

3. f(t)F(p-) -теорема смещения.