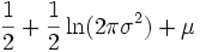Моделирование логнормального распределения

Рефераты / Программирование, компьютеры и кибернетика / Моделирование логнормального распределения

Заключение

В моей работе я рассмотрел логнормальное распределение, мы получили графики плотности распределения и функции распределения, и связи с другими распределениями.

В результате работы был создан программный продукт в среде Delphi 7, где мы можем посмотреть как моделируется логнормальное распределение, выводятся графики плотности распределения при помощи

аналитических расчетов и стохастических преобразований. А также вычисляется мат. ожидание и дисперсия, стохастическим и аналитическим способами.

Список используемой литературы

1. http://en.wikipedia.org

2. Шеффе Г. Дисперсионный анализ. - М.: Физматгиз, 1980. - 628 с.

3. «Delphi 2005: «Секреты программирования»», Михаил Фленов.

Общие данные логнормальное распределение
Плотность вероятности μ=0
Функция распределения μ=0
Параметры	$\sigma \ge 0$ $-\infty \le \mu \le \infty$
Носитель	$x \in [0; +\infty)\!$
Плотность вероятности	$\exp\left(-\left.\left[\frac{\ln(x)-\mu}{\sigma}\right]^2\right/2\right) \left/ \left(x\sigma\sqrt{2\pi}\right) \right.$
Функция распределения	$\frac{1}{2}+\frac{1}{2} \mathrm{Erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]$
Математическое ожидание	$e^{\mu+\sigma^2/2}$
Медиана	eμ
Мода	$e^{\mu-\sigma^2}$
Дисперсия	$(e^{\sigma^2}\!\!-1) e^{2\mu+\sigma^2}$
Коэффициент асимметрии	$e^{-\mu-\sigma^2/2}(e^{\sigma^2}\!\!+2)\sqrt{e^{\sigma^2}\!\!-1}$
Коэффициент эксцесса	$e^{4\sigma^2}\!\!+2e^{3\sigma^2}\!\!+3e^{2\sigma^2}\!\!-6$
Информационная энтропия	$\frac{1}{2}+\frac{1}{2}\ln(2\pi\sigma^2) + \mu$

Логнорма́льное распределе́ние в теории вероятностей - это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то её логарифм имеет нормальное распределение.

Определение

Пусть распределение случайной величины X задаётся плотностью вероятности, имеющей вид:

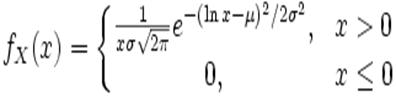$f_X(x) = \left\{ \begin{matrix} \frac{1}{x \sigma \sqrt{2 \pi}} e^{-(\ln x - \mu)^2/2\sigma^2}, & x > 0 \\ 0, & x \le 0 \end{matrix} \right.$ ,

где $\sigma>0,\; \mu\in \mathbb{R}$ . Тогда говорят, что X имеет логнормальное распределение с параметрами μ и σ. Пишут: X˜LogN(μ,σ2).

Моменты

Формула для k-го момента логнормальной случайной величины X имеет вид:

$\mathbb{E}\left[X^k\right] = e^{k\mu + \frac{k^2\sigma^2}{2}},\; k \in \mathbb{N},$

откуда в частности:

$\mathbb{E}[X] = e^{\mu + {\sigma^2 \over 2}}$ ,

$\mathrm{D}[X] =\left(e^{\sigma^2}-1\right) e^{2\mu + \sigma^2}$ .

Свойства логнормального распределения

· Если $X_1,\ldots, X_n$ - независимые логнормальные случайные величины, такие что $X_i \sim \mathrm{LogN}(\mu, \sigma_i^2)$ , то их произведение также логнормально:

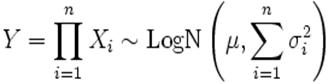$Y = \prod\limits_{i=1}^n X_i \sim \mathrm{LogN}\left(\mu, \sum\limits_{i=1}^n \sigma^2_i\right)$ .

Связь с другими распределениями

· Если X˜LogN(μ,σ2), то

Y = lnX˜N(μ,σ2).

Скачать реферат

Страница: 1 2 3

Моделирование логнормального распределения

Другие рефераты на тему «Программирование, компьютеры и кибернетика»:

Поиск рефератов

Последние рефераты раздела

document.write('<p class="otherfont" style="float:right; color:#222222; text-align:center;">Страница <br /><big style="font-size:18px;"><b>3</b></big></p>'); Моделирование логнормального распределения

Другие рефераты на тему «Программирование, компьютеры и кибернетика»:

Поиск рефератов

Последние рефераты раздела

Моделирование логнормального распределения