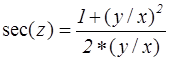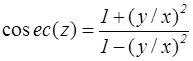Дополнительные арифметические команды

Таблица 3 – Формулы для вычисления тригонометрических функций

3. команды управления сопроцессора х87

В СОПРОЦЕССОРАХ 387+ появились новые команды:

Ø FSIN – вычисление синуса;

Ø FCOS – вычисление косинуса;

Ø FSINCOS – вычисление синуса и косинуса.

Все они воспринимают в ST(0) исходный угол, измеряемый в радианах и находящийся в диапазоне: –263 <= ST(0) <= +263. Команды FSIN и FCOS возвращают результат на место аргумента, а команда FSINCOS возвращает значение синуса на место аргумента и включает значение косинуса в стек.

Команда FPATAN вычисляет arctg (ST(1)/ST(0)). Два операнда извлекаются из стека, а результат включается в стек. Поэтому окончательно, УКАЗАТЕЛЬ СТЕКА УВЕЛИЧИВАЕТСЯ НА 1. Операнды этой команды для сопроцессоров 8087/287 должны удовлетворять условию:

0 < ST(1) < ST(0).

В сопроцессорах 387+ ограничений на диапазон допустимых аргументов команды FPATAN не существует.

Для вычисления остальных обратных тригонометрических функций по аргументу «z» необходимо предварительно подготовить операнды в ST(0) и ST(1) в соответствии с табл. 4 (делить операнды не нужно).

Таблица 4 – Формулы для вычисления обратных тригонометрических функций

←ST(1) ←ST(0)
←ST(1) ←ST(0)
←ST(1) ←ST(0)	←ST(1) ←ST(0)
←ST(1) ←ST(0)
←ST(1) ←ST(0)

Команда FYL2X вычисляет функцию: ST(1) * log2 ST(0). Два операнда извлекаются из стека, а затем результат включается в стек. Поэтому УКАЗАТЕЛЬ СТЕКА УВЕЛИЧИТСЯ НА 1. В команде требуется удовлетворение естественного для логарифмической функции условия:

ST(0) > 0.

Значения других логарифмических функций вычисляются по формулам в табл. 5 с загрузкой в регистр ST(1) необходимых констант командами: FLDLN2 и FLDLG2.

Таблица 5 - Формулы для вычисления логарифмических функций

Еще одна логарифмическая команда FYL2XP1 вычисляет функцию: ST(1) * log2 (ST(0) + 1). Причина появления этой команды заключается в получении более высокой точности вычисления функции: log(1 + x). Эта функция часто встречается в финансовых расчетах, а также при вычислении обратных гиперболических функций.

Команда показательной функции F2XM1 вычисляет:

F2XM1 [ST(0)] = 2(ST(0)) – 1.

Аргумент показательной функции должен находится в диапазоне: для сопроцессоров 87/287: 0 <= ST(0) <= 0.5;

для сопроцессоров 387+: –1 <= ST(0) <= +1.

Вычисление функции 2х – 1 вместо функции 2х позволяет избежать потери точности, когда аргумент «х» близок к 0 (а значение функции 2х близко к 1). Остальные показательные функции вычисляются по формулам в табл. 6.

Таблица 6 – Формулы для вычисления показательных функций

Таблица 7 – Формулы для вычисления гиперболических функций

 Скачать реферат