Моделирование динамики яркостной температуры земли методом инвариантного погружения и нейронных сетей

Для большинства реальных задач бывает достаточным нескольких сотен или тысяч наблюдений. Для сложных задач может потребоваться большее количество, однако очень редко встречаются задачи, где требуется менее 100 наблюдений. Если данных мало, то сеть не имеет достаточной информации для обучения, и лучшее, что можно в этом случае сделать, – это попробовать подогнать к данным некоторую линейную моде

ль.

После того как определено количество слоев сети и число нейронов в каждом из них, нужно назначить значения весов и смещений, которые минимизируют ошибку решения. Это достигается с помощью процедур обучения. Путем анализа имеющихся в распоряжении аналитика входных и выходных данных веса и смещения сети автоматически настраиваются так, чтобы минимизировать разность между желаемым сигналом и полученным на выходе в результате моделирования. Эта разность носит название ошибки обучения. Таким образом, процесс обучения – это процесс подгонки параметров той модели процесса или явления, которая реализуется нейронной сетью. Ошибка обучения для конкретной конфигурации нейронной сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения выходных значений с желаемыми, целевыми значениями. Эти разности позволяют сформировать так называемую функцию ошибок (критерий качества обучения). В качестве такой функции чаще всего берется сумма квадратов ошибок. При моделировании нейронных сетей с линейными функциями активации нейронов можно построить алгоритм, гарантирующий достижение абсолютного минимума ошибки обучения. Для нейронных сетей с нелинейными функциями активации в общем случае нельзя гарантировать достижения глобального минимума функции ошибки.

При таком подходе к процедуре обучения может оказаться полезным геометрический анализ поверхности функции ошибок. Определим веса и смещения как свободные параметры модели и их общее число обозначим через N; каждому набору таких параметров поставим в соответствие одно измерение в виде ошибки сети. Тогда для всевозможных сочетаний весов и смещений соответствующую ошибку сети можно изобразить точкой в ЛЧ-1 – мерном пространстве, а все такие точки образуют некоторую поверхность, называемую поверхностью функции ошибок. При таком подходе цель обучения нейронной сети состоит в том, чтобы найти на этой многомерной поверхности глобальный минимум.

В случае линейной модели сети и функции ошибок в виде суммы квадратов такая поверхность будет представлять собой параболоид, который имеет единственный минимум, и это позволяет отыскать такой минимум достаточно просто.

В случае нелинейной модели поверхность ошибок имеет гораздо более сложное строение и обладает рядом неблагоприятных свойств, в частности может иметь локальные минимумы, плоские участки, седловые точки и длинные узкие овраги.

Определить глобальный минимум многомерной функции аналитически невозможно, и поэтому обучение нейронной сети, по сути дела, является процедурой изучения поверхности функции ошибок. Отталкиваясь от случайно выбранной точки на поверхности функции ошибок, алгоритм обучения постепенно отыскивает глобальный минимум. Как правило, для этого вычисляется градиент (наклон) функции ошибок в данной точке, а затем эта информация используется для продвижения вниз по склону. В конце концов алгоритм останавливается в некотором минимуме, который может оказаться лишь локальным минимумом, а если повезет, то и глобальным.

Таким образом, по существу алгоритмы обучения нейронных сетей аналогичны алгоритмам поиска глобального экстремума функции многих переменных.

Итак,преимущества нейросетевого подходазаключаются в следующем:

• параллелизм обработки информации;

• единый и эффективный принцип обучения;

• надежность функционирования;

• способность решать неформализованные задачи.

3. Моделирование динамики яркостной температуры методом инвариантных погружений и нейронных сетей

3.1 Получение экспериментальных данных на производственной практике

Одним из типов исследований методом радиометрического дистанционного зондирования земли является полевой эксперимент. Радиометрический комплекс установленный на агробиологической станции Омского Государственного Педагогического Университета состоит из трех радиометров частот 2,73Gh, 6,0Gh, 8,15Gh с соответственной длинной волны 11 см, 5 см и 3,6 см. (рис. 1, рис. 2), устанавливаемых на передвижном штативе (раме), передвижной лаборатории и 6 экспериментальных участков размером 1,4 м * 1,4 м (рис. 3).

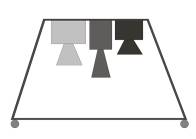
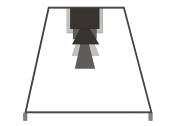
Рис. 3. Схема передвижного штатива с радиометрами

Рис. 4. Передвижение рамы с радиометрами с одного участка на другой

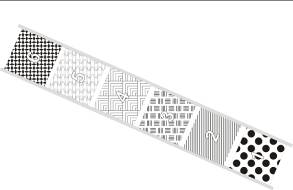
Рис. 5. Экспериментальные участки

Конструкция и размеры передвижного штатива (рамы) были выбраны исходя из удовлетворения следующим критериям [1]:

1. Эталоны и исследуемые участки должны находиться в дальней зоне антенн радиометров

2. Ширина главного лепестка по уровню 0,5 дб должна быть меньше геометрических размеров, эталонов и участков.

3. Угол наклона антенн должен составлять 100

Участки №1, №2, №3, №4 являются экспериментальными участками, на которых расположены следующие виды почв: земля, загрязненная нефтью, песок, глина, чернозем, соответственно. На участке №5 расположен лист металла, а на участке №6 – емкость с водой. Участки №5 и №6 используются для калибровки оборудования, а измерения снятые с этих участков являются опорной точкой (калибровкой) для расчета яркостных температур почвы участков №1 – №4.

Штатив (рама) передвигается с одного на другой участок, измерения проводятся последовательно радиометрами с частотой 5 Gh, затем 11 Gh, затем 3,6 Gh.

При калибровке радиометров используются следующие эталоны излучения: излучения неба, отраженное металлическим листом, излучение гладкой водной поверхности, излучение поглощающего покрытия. Размеры эталонов должны превышать размеры пятна, излучающего в главный лепесток, чтобы дифракционными явлениями на краях образцов можно пренебречь.

В ходе эксперимента замерялись: время, температура окружающей среды, температура слоя почвы на глубине 0,5 см и 2 см, а также измерялась яркостная температура почв.

Дважды в день брались пробы почв на влажность: поверхностный слой 0–1 см, 1–2 см, и 3–4 см.

Исследуемыми объектами являлись участки №2 и №3, песчаная и глинистая почва соответственно (рис. 4; рис. 5).

Рис. 6. Песчаная почва. Участок №2

Рис. 7. Средний суглинок. Участок №3

Из полученных данных видно, что почти одинаковые в оптическом диапазоне почвы, кардинально отличаются по физическим свойствам.

Таблица 1. Гранулометрический состав почв (% от массы сухой почвы)

 Скачать реферат