Линейные электрические цепи

Δ1= 37,5 315 – 90 = 2 187 060,75 + 2 278 812,5 +

0 – 90 277,5

+ 797 343,75 – 202 662 + 1 717 031,25 = 4 726 586,25

252 25,02 – 67,5

Δ2= – 165 37,5 – 90 = 2 622 375 + 151 996,5 –

– 67,5 0 277,5

– 170 859,375 + 1 145 603,25 = 3 749 115,

375

252 – 165 25,02

Δ3= – 165 315 37,5 = 371 547 + 417 656,25 + 531 987,75 +

– 67,5 – 90 0

+ 850 500 = 2 171 691

5. Определяем контурные токи

I1.1 = Δ1/ Δ = 0,526

I2.2 = Δ2/ Δ = 0,417

I3.3 = Δ3/ Δ = 0,242

6. Используя II закон Кирхгофа, определяем токи в цепях

ί1= I1.1 = 0,526 А ί4= I3.3 = 0,242 А

ί2= I2.2 = 0,417 А ί5= I2.2 – I1.1 = – 0,109 А

ί3= I2.2 – I3.3 = 0,175 А ί6= I1.1 – I3.3 = 0,284 А

7. Проверка

ί5+ ί1– ί2= – 0,109 + 0,526 – 0,417 = 0

ί3– ί6– ί5= 0,175 – 0,284 + 0,109 = 0

ί6+ ί4– ί1= 0,284 + 0,242 – 0,526 = 0

ί2– ί3– ί4= 0,417 – 0,175 – 0,242 = 0

Метод узловых потенциалов

Дано:

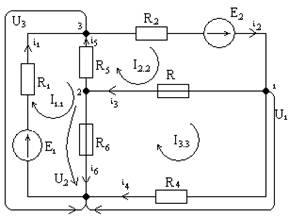R1= 19,5 Ом E1 = 25,8 В

R2 = 60 Ом E2 = 37,5 В

R3 = 90 Ом E3 = 0 В

R4.1 = 150 Ом I1 = 0,04 А

R4.2 = 600 Ом I2 = 0 А

R5 = 165 Ом I3 = 0 А

R6.1 = 40 Ом R6.2 = 27,5 Ом

Решение:

1. Определяем собственную проводимость узла, которая равна сумме проводимостей, сходящихся в узле

g1= 1 / R1= 0,05 g4= 1 / R4= 0,01

g2= 1 / R2= 0,02 g5= 1 / R5= 0,01

g3= 1 / R3= 0,01 g6= 1 / R6= 0,01

2. Определяем взаимную проводимость в узле, которая равна проводимости ветви, соединяющей два узла

g1.1= g4+ g2+ g3= 0,04 g1.2= g2.1= g3= 0,01

g2.2= g3 + g5+ g6= 0,03 g2.3= g3.2= g5= 0,01

g3.3= g1+ g2+ g5= 0,08 g1.3= g3.1= g2= 0,02

3. Определяем сумму токов от источников, которые находятся в ветвях, сходящихся в данном узле

I1.1= – E2/ R2 = – 37,5 / 60 = – 0,625

I2.2= 0

I3.3= E1 / R1+ E2 / R2 = 25,02 / 19,5 + 37,5 / 60 = 1,905

4. Записываем в общем виде систему уравнений

u1· g1.1– u2· g1.2– u3· g1.3= I1.1

– u1· g2.1+ u2· g2.2– u3· g2.3= I2.2

– u1· g3.1– u2· g3.2+ u3· g3.3= I3.3

5. Переписываем систему уравнений с числовыми коэффициентами

0,04 u1– 0,01 u2– 0,02 u3= – 0,63

– 0,01 u1+ 0,03 u2– 0,01 u3= 0

– 0,02 u1– 0,01 u2+ 0,08 u3= 1,91

6. Считаем определители системы

0,04 – 0,01 – 0,02

Δ = – 0,01 0,03 – 0,01 = 0,000096 – 0,000002 – 0,000002 –

– 0,02 – 0,01 0,08

– 0,000012 – 0,000004 – 0,000008 = 0,000068

– 0,63 – 0,01 – 0,02

Δ1= 0 0,03 – 0,01 = – 0,001512 + 0,000191 + 0,001146 +

1,91 – 0,01 0,08

+ 0,000063 = – 0,000112

0,04 – 0,63 – 0,02

Δ2= – 0,01 0 – 0,01 = – 0,000126 + 0,000382 + 0,000764 –

– 0,02 1,91 0,08

– 0,000504 = 0,000516

0,04 – 0,01 – 0,63

Δ3= 0,01 0,03 0 = 0,002292 – 0,000063 – 0,000378 –

– 0,02 – 0,01 1,91

– 0,000191 = 0,00166

7. Определяем узловые напряжения

U1.1= Δ1/ Δ = – 1,647 В

U2.2= Δ2/ Δ = 7,588 В

U3.3= Δ3/ Δ = 24,412 В

8. Используя II закон Кирхгофа, определяем токи в ветвях

ί1= (E1 – U3) / R1= (25,02 – 24,412) / 19,5 = 0,03 А

ί2= (– E2 – U1 + U3) / R2= (– 37,5 + 1,647 + 24,412) / 60 = – 0,19 А

ί3= (U1 – U2) / R3= (– 1,647 – 7,588) / 90 = – 0,1 А

ί4= U1 / R4= – 1,647 / 120 = – 0,01 А

ί5= (– U3 + U2) / R5= (– 24,412 + 7,588) / 165 = – 0,1 А

ί6= U2/ R6= 7,588 / 67,5 = 0,11 А

9. Проверка

ί5+ ί1– ί2= – 0,1 + 0,03 + 0,191 = 0,12

ί3– ί6– ί5= – 0,1 – 0,11 + 0,11 = – 0,11

ί6+ ί4– ί1= 0,11 – 0,01 – 0,03 = 0,07

ί2 – ί3 – ί4 = – 0,19 + 0,1 + 0,01 = – 0,08

ЗАДАЧА 2 Линейные электрические цепи синусоидального тока

В сеть переменного тока с действующим значением напряжения U включена цепь, состоящая из двух параллельных ветвей. Определить показания приборов, реактивную мощность цепи, коэффициент мощности и построить векторную диаграмму напряжений. Указать на схеме положительное направление токов в ветвях и обозначить эти токи.

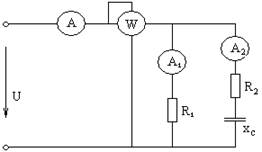
Дано:

R1= 8 Ом

R2 = 2 Ом

U = 127 В

јx c= 17 Ом

Решение:

1. Примем начальную фазу напряжения равной нулю

Ů = 127 е ј0В

2. Определяем комплексное сопротивление

z 1= R1= 8 Ом

z 2= R2– јx c= √2 2+ 17 2 · е – ј arctg17/4= 17,1 е – 77

3. По закону Ома определяем комплексные точки

İ 1= Ů / z 1= 127 е ј0/ 8 = 15,9 е ј0А

İ 2= Ů / z 2= 127 е ј0/ 17,1 е – 77= 7,4 е ј 77=

= 7,4 · cos 77 + ј 7,4 · sin 77 = 1,7 + ј 7,2

4. Определяем полный комплексный ток

İ = İ 1+ İ 2= 15,9 е ј0+ 7,4 е ј 77= 15,9 cos 0 + ј 15,9 sin 0 +

+ 7,4 cos 77 + ј 7,4 sin 77 = 17,5 + ј 7,2 =

= √17,5 2+ 7,2 2· е ј arctg7,23/17,544 = 18,9 · е ј 22

А 18,9 А

А1 15,9 А

А2 7,4 А

5. Определяем полную мощность

S = İ · Ů = 18,9 е ј 22· 127 е ј0= 2410,5 е ј 22 =

= 2410,5 cos 22 + ј 2410,5 sin 22 = 2234,9 + ј 902,9

İ = 18,9 · е ј22 S = 2410,5 ВА

P = 2234,9 Вт Q = 902,9 ВАР

6. Определяем коэффициент мощности

cos φ = P / S = 0,93

ЗАДАЧА 3 Линейные электрические цепи синусоидального тока

В цепь переменного тока с мгновенным значением напряжения

 Скачать реферат