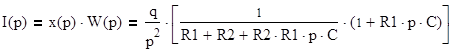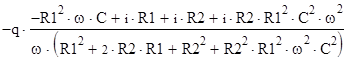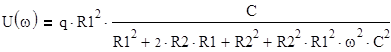Исследование модели электролитического осаждения меди

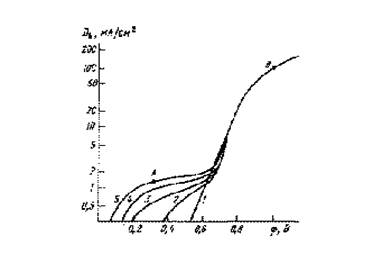
Рисунок 3.4 Зависимость плотности тока осаждения меди от потенциала катода для электролитов с различной концентрацией ионов Cu2+ [4]

Для получения многослойных структур необходимо на катод электролитической ванны периодически подавать импульсы напряжения разной амплитуды и длительности, в течение которых на катоде будет

осаждаться соответствующий металл. В зависимости от режимов подачи импульсов различают потенциостатическое и гальваностатическое импульсное электролитическое осаждение. При гальваностатическом осаждении на катоде поддерживается постоянной в течение каждого импульса плотность тока. Так, при получении Cu-Ni многослойных структур [5] плотность тока при осаждении слоя меди составляла 1,5 мА/см2, в то время как при осаждении слоя никеля плотность тока поддерживалась равной 100 мА/см2. В потенциостатическом режиме постоянными на катоде поддерживались напряжения: 400 мВ для меди и 1000 мВ для никеля. При длительности импульсов 5,5 с и 0,2 с при осаждении Cu и Ni соответственно формировались слои этих металлов одинаковой толщины по 100 Å.

Потенциостатический режим осаждения в большинстве случаев позволяет получать более резкую границу между слоями в магнитных многослойных структурах. При оптимальном выборе режимов электролитического осаждения содержание магнитного элемента в немагнитном и наоборот может не превышать 0,5…0,1 % [4].

3 Построение физико-математической модели

a) найдем ток, протекающий через установку:

б) найдем количество меди и передаточную функцию:

в) построим физико-математическую модель:

4 Определение характеристик

а) зависимость тока от времени, используя преобразование Лапласа

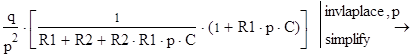
б) частотные характеристики ТС

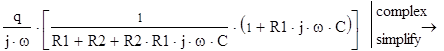
действительная часть:

мнимая часть:

5 Общие нелинейные дифференциальные уравнения

Пусть u=u(x1,x2,…,xn) – функция, определенная в любой точке действительных чисел. Градиентом u является N - вектор-функция, обозначаемая grad u и определенная следующим образом:

(1)

В дальнейшем будем прежде всего иметь дело с функциями, определенны­ми в плоских областях, т.е. при N = 2. Для функции u = u (х, у) имеем

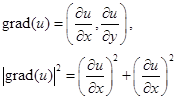(2)

5.1 Нелинейный оператор Лапласа

Рассмотрим плоскую область и функцию и =и(х,у), удовлетворяющую уравнению

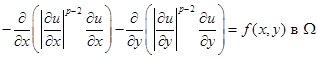(3)

 Скачать реферат