Дрейфовые транзисторы их параметры, преимущества и недостатки

(2.2.4)

(2.2.5)

Известно,[4] что при низком уровне инжекции заряд электронов в базе Qn пропорционален сквозному току 1пх. Коэффициент пропорциональности представляет собой постоянную накопления заряда электронов в базе и определяется (2.1.23). При высоком уро

вне инжекции [п(х)>>|N(х)|] пропорциональность между Qn и Inx по-прежнему сохраняется, но коэффициент пропорциональности имеет другое значение, определяемое формулой [3]:

(2.2.6)

В общем случае

(2.2.7)

где т=т(η) при низком уровне инжекции и т=2 при высоком уровне инжекции электронов в базе.

Выражение (2.2.2) с учетом (2.2.4) , (2.2.5) и (2.2.7) можно представить в виде

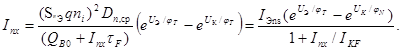(2.2.8)

В (2.2.8) обозначено

; (2.2.9)

(2.2.10)

Ток /Эns определяет электронную составляющую тока насыщения эмиттерного р-п перехода при низком уровне инжекции. Ток ikf является характеристическим током, определяющим границу между низким и высоким уровнями инжекции электронов в базе.

Далее будем рассматривать нормальный активный режим. Для этого режима UK<<-φT, и поэтому

(2.2.11)

Использовав (2.2.11), можно установить связь между напряжением Uэ и сквозным током Inx.

(2.2.12)

Определим ток объемной рекомбинации электронов в базе, В соответствии с [4] этот ток

(2.2.13)

Время жизни электронов зависит от концентрации легирующих примесей [4], а поэтому и от координаты. Тогда в соответствии с [4] запишем

(2.2.14)

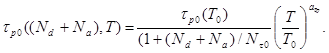(2.2.15)

где τпо(То), τро(Tо) определяются при Tо=300 К.

При высоком уровне инжекции можно считать, что концентрация электронов в базе уменьшается практически линейно от ее значения nрэ у эмиттера до нуля у коллектора:

(2.2.16)

Кроме того, при высоком уровне инжекции

(2.2.17)

С учетом этих предположений можно ввести эффективное (усредненное) время жизни электронов в базе в соответствии с выражением

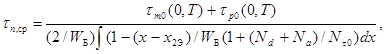(2.2.18)

где интегрирование проводится в пределах квазиэлектронейтральной базы от x2Э до x1K.

С учетом (2.2.18) и (2.2.7) ток объемной рекомбинации электронов в базе определяется выражением

(2.2.19)

Для расчета коэффициента передачи тока необходимо определить ток дырок, инжектированных из р-базы в п+-эмиттер. Дырки, проникающие в эмиттер дрейфового транзистора, перемещаются в нем не только за счет диффузии, но и под действием электрического поля, обусловленного неоднородным легированием эмиттера, а также эффектом сужения запрещенной зоны в сильнолегированном эмиттере. В состоянии термодинамического равновесия ток электронов эмиттера равен нулю. Положим в уравнении [4]

(2.2.20)

где ∆φG=∆EG/q, ∆EG-сужение запрещенной зоны;

A- коэффициент асимметрии в сужении (А=0,5).

Jnx=0 и использовав соотношение Эйнштейна, выразим напряженность электрического поля:

(2.2.21)

Подставив (2.2.21) в уравнение для плотности тока дырок [4],

(2.2.22)

получим (2.2.23)

Дрейфовый ток дырок пропорционален эффективной напряженности электрического поля для дырок[4]:

(2.2.24)

Первый член в этом выражении является «классической» составляющей напряженности электрического поля, обусловленного неоднородным легированием. Второй член отражает наличие добавочной силы, связанной с изменением валентных сил в кристалле, обусловленных сильным легированием (эффект СЗЗ). Для транзистора с распределением концентрации легирующих примесей, показанным на рис. 2.1.1, первая составляющая поля Ep1 при НУИ направлена по оси х и тормозит дырки, инжектированные в эмиттер. Вторая составляющая поля Ep2<0 и уменьшает тормозящее поле для дырок в эмиттере. Таким образом, влияние СЗЗ приводит к дополнительному накоплению заряда дырок в эмиттере, увеличению концентрации дырок дырочного тока эмиттера и к уменьшению коэффициента инжекции.

Распределение электрического поля и концентрация дырок в эмиттере.

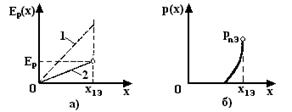
Рис.2.2.1

Примерное распределение Ер(х) в квазиэлектронейтральной области эмиттера показано на рис. 2.2.1,а. Без учета сужения запрещенной зоны Ep1 определяется кривой 1, а с учетом — кривой 2. Обычно при низком уровне инжекции тормозящее электрическое поле достаточно велико, и дырки, диффундирующие против поля, проникают в эмиттер на небольшое расстояние, на котором Ер мало изменяется. Для оценочного расчета р(х) будем полагать, что на этом расстоянии электрическое поле Ер, коэффициент диффузии дырок Dp и их время жизни τр постоянны и соответствуют значениям, рассчитанным при х=х1Э. Подставив (2.2.23) в уравнение непрерывности для дырок[4]

(2.2.25)

получим для стационарного режима

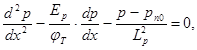(2.2.26)

где— диффузионная длина дырок.

Приближенное решение этого дифференциального уравнения имеет вид

(2.2.27)

где рпэ ==р(х1Э)) — концентрация дырок при х=х1э (рис. 2.2.1,6).

В этом случае характеристическая длина L*, на которой концентрация дырок спадает в е раз, называется диффузионной длиной против поля. Она определяется выражением

(2.2.28)

где ηЭ=EpLp/φTфактор поля; функция

, при ηЭ»1.

Таким образом, при низком уровне инжекции дырочный ток эмиттера (при x=x1Э) определяется выражением

 Скачать реферат