Внутренние силы и напряжения, возникающие в поперечных сечениях бруса при растяжении и сжатии

В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность междунапряжениями и деформациями:

Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода. Модуль упругости является физ

ической, константой материала и определяется путем эксперимента. Величина Е измеряется в тех же единицах, что и а, т. е. в кГ/см2. Для наиболее часто применяемых материалов модуль упругости имеет следующие значения в кГ/см2:

Закон Гука является приближенным. Для некоторых материалов, таких, как, например, сталь, он соблюдается с большой степенью точности в широких пределах изменения напряжений. В некоторых же случаях наблюдаются заметные отклонения от закона Гука. Например, для чугуна и некоторых строительных материалов даже при малых напряжениях закон Гука может быть принят только в грубом приближении. В тех случаях, когда закон Гука явно не соблюдается, деформацию задают в виде некоторой нелинейной функции от напряжения

с таким расчетом, чтобы эта функция отвечала кривой, полученной из испытания материала.

Вернемся к выражению (1.4) и заменим в нем о на , а е на Тогда получим

Абсолютное удлинение стержня на длине l будет равно

В том случае, когда стержень нагружен только по концам, нормальная сила N = Р не зависит от г. Если, кроме того, стержень имеет постоянные размеры поперечного сечения Р, то из выражения (1.5) получаем

При решении многих практических задач возникает необходимость наряду с удлинениями, обусловленными напряжением учитывать также удлинения, связанные с температурным воздействием. В этом случае пользуются способом наложения и деформацию е рассматривают как сумму силовой деформации и чисто температурной деформации:

где а — коэффициент температурного расширения материала.

Для однородного стержня, нагруженного по концам и равномерно нагретого, получаем, очевидно,

Таким образом, силовая и температурная деформации рассматриваются как независимые. Основанием к этому служит экспериментально установленный факт, что модуль упругости Е при умеренном нагреве слабо меняется с температурой, точно так же как и величина а практически не зависит от напряженияДля стали это имеет место до температуры порядка 300—400° С. При более высоких температурах необходимо учитывать зависимость

Рассмотрим примеры определения напряжений и перемещений в некоторых простейших случаях растяжения и сжатия.

Пример 1.1. Требуется выявить закон изменения нормальных сил, напряжений и перемещений по длине ступенчатого стержня, нагруженного на конце силой Р (рис. 21, а), определить числовые значения наибольшего напряжения и наибольшего перемещения, еслиМатериал — сталь,

Поскольку сила Р велика, собственный вес стержня не имеет значения.

Из условий равновесия любой отсеченной части стержня вытекает, что нормальная сила N в каждом сечении стержня численно равна внешней силе Р. Построим график изменения силы N вдоль оси стержня. Графики подобного рода называются в сопротивлении материалов эпюрами. Они Дают наглядное представление о законах изменения различных исследуемых величин. В данном случае эпюра нормальной силы представлена на рис. 21, б прямоугольником, посколькуНа рисунке эпюра N заштрихована линиями, которые проведены в направлении откладываемой на графике величины N. В данном случае значение силы N откладывается вверх, следовательно, штриховка проведена Вертикально.

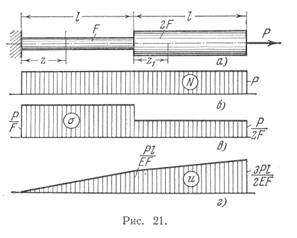
Для того чтобы получить эпюру напряжений 0, надо ординаты эпюры N изменить обратно пропорционально величине Р (рис. 21, е). Большее значение о равно

Определим, на какую величину и (см) переместится каждое сечение стержня по направлению силы Р. Перемещениесечения равно удлинению отрезка

Длиной Следовательно, согласно формуле (1.6)

Таким образом, на участке изменения перемещение и пропорционально г (рис. 21, г). На втором участке стержня перемещение равно

Зависимостьтакже будет линейной. Наибольшее перемещение имеет торцевое сечение стержня

Пример 1.2. Построить эпюры нормальных сил, напряжений и перемещений для свободно подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 22). Длина стержня площадь поперечного сечения Р, удельный вес материалаНормальная сила в сеченииравна весу нижележащей части стержня: Следовательно, нормальная сила пропорциональнаЭпюра. А в данном случае штрихуется горизонтальными линиями, поскольку величины N откладываются в горизонтальном направлении. Напряжение в сечении равно (см. эпюру на рис. 22).

 Скачать реферат