Экономико-математические методы маркетингового исследования
2) Из всех дуг уже зафиксированных для множества y составляем связный путь, который обязательно включает в себя последнюю зафиксированную дугу ![]() . Этот связный путь может состоять из одной дуги
. Этот связный путь может состоять из одной дуги ![]() . Полагаем, что в матрице
. Полагаем, что в матрице ![]()
![]() , где m – конец, а p – начало, т.е. запрещаем подциклы.
, где m – конец, а p – начало, т.е. запрещаем подциклы.
3) Приводим ![]() , в результате получим
, в результате получим ![]() с
с ![]() – константа приведения.
– константа приведения.
Схема получения ![]()
1) в матрице ![]() полагаем, что
полагаем, что ![]() , т.е. запрещаем.
, т.е. запрещаем.
2) В результате получаем ![]() , приводим
, приводим ![]() , получаем
, получаем ![]() и
и ![]()
Схема выбора дуги ![]()
1) просматривая все нулевые элементы ![]() , и для каждого такого элемента рассчитываем величину
, и для каждого такого элемента рассчитываем величину ![]() – сумма минимального элемента i-ой строки и минимального элемента j-го столбца матрицы
– сумма минимального элемента i-ой строки и минимального элемента j-го столбца матрицы ![]() , исключая сам нулевой элемент.
, исключая сам нулевой элемент. ![]() .
.
2) ![]() выбираем из условия
выбираем из условия ![]() для всех
для всех ![]()
![]() можно не получать, а сразу получать
можно не получать, а сразу получать ![]() .
.
Если же в процессе решения задачи придется разбивать ![]() , а соответствующей матрицы нет, то её нужно восстановить из исходной матрицы.
, а соответствующей матрицы нет, то её нужно восстановить из исходной матрицы.
Схема восстановления ![]() для любого X из исходной матрицы
для любого X из исходной матрицы ![]() :
:
Пусть вершина X такова, что для неё уже зафиксированы ![]() .
.
Шаг 1: для каждой фиксированной дуги ![]()
![]() для каждой
для каждой ![]() .
.
Шаг 2: для каждой фиксированной дуги ![]() составляет связный путь, который содержит обязательную дугу
составляет связный путь, который содержит обязательную дугу ![]() ; и запрещает переезд из
; и запрещает переезд из ![]() в
в ![]() , т.е.
, т.е. ![]() , где m – коней и p – начало.
, где m – коней и p – начало.
Шаг 3: для каждой запрещенной дуги ![]() полагаем, что
полагаем, что ![]()
В результате получаем матрицу ![]() , приводим её и получаем
, приводим её и получаем ![]() .
.
Связной путь должен содержать последнюю зафиксированную дугу.
Пример
Фирма «Турал Арбуз Корпорейшен» проводит исследование для более удачного расположения нового склада для товара, который они должны поставлять в 4 магазина. Одним из критериев выбора стала своевременная поставка товара в кротчайшие сроки (обговорено в контрактах). Т.е. получается задача о коммивояжере. Водитель должен побывать на каждой точке с утра и вернуться на склад. Продается три склада, нужно выбрать один из них (цены одинаковы). Важнейшим критерием является минимальный срок проезда через все магазины и возвращение опять на склад. Известно время, за которое водитель может доехать с одной торговой точки до другой и время проезда до склада. Сначала находим минимальное время пути, затрачиваемое водителем с первого склада.
Дана матрица затрачиваемого времени при переезде из точки i в j.

Приведение матрицы ![]() по строкам:
по строкам:
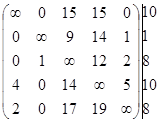
Приведение матрицы по столбцам:
![]()
![]()
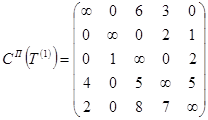
![]()
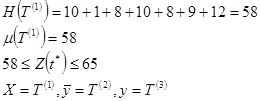
Выбираем ![]() :
:

Получаем матрицу ![]()
Связной путь (2,3), следовательно ![]()
![]()
![]()
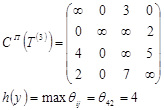
Начинаем 2-ую итерацию
![]()
Связной путь: ![]()

3-я итерация.
![]()
Нам нужно восстановить ![]() из
из ![]()
![]()
![]()
![]()
![]()

![]() – связной путь
– связной путь ![]() ,
, ![]()
