Экономико-математические методы маркетингового исследования

Дальнейший процесс решения задачи можно построить двумя способами.

Граф:

Первый способ:

Для дальнейшего разбиения выбирается подмножество из подмножеств, полученных в результате последнего разбиения , например:

Пусть это будет width=65 height=27 src="images/referats/7343/image039.png">и производим разбиение.

Дальнейший процесс будет проходить также.

При этом способе можно достаточно быстро получить подмножество , содержащее всего один план задачи

, то - претендент на оптимальный план. Запоминаем на графе на ветке, приводящей к ставим конец и корректируется величина , т.е. .

увеличена, следовательно нужно рассмотреть все нерассмотренные подмножества.

Далее продолжаем процесс решения задачи также.

Второй способ:

Выбирается множество для разбиения из всех висячих вершин, ещё нерассмотренных.

Выбирать способ решения задачи нужно в зависимости от конкретной задачи. При любом способе решения процесс продолжаем до тех пор пока не будет выполнено следующее условие: для любого (висячие вершины).

Решением задачи будет тот план, который дал последнее значение величине .

Для решения конкретной ЗДП необходимо строить алгоритм метода ветвей и границ, согласно приведенной схеме. При этом нужно решить следующие проблемы:

1) как найти ;

2) по какому принципу проводить разбиение множества;

3) как вычислить .

Решение задачи о комивояжере.

– верхняя оценка оптимального значения

– нижняя оценка функции цели на множестве

- оптимальная

Как найти ?

Для нахождения необходимо провести операцию приведения матрицы .

Определение:

Процесс вычитания из каждого элемента i-ой строки матрицы минимального элемента этой строки называется приведением матрицы по строке I, а минимальный элемент этой строки называется константой приведения. Аналогично процесс вычитания из каждого элемента j-ого столбца матрицы называется приведением матрицы по столбцам.

Приведенная матрица – это матрица, которая приведена и по всем строкам и столбцам.

– суммарная константа приведения матрицы .

Критерий приведения – в каждой строке и столбце должны быть хотя бы один нуль.

Приведенная матрица –

t – произвольный гамельктоновый цикл.

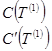
На каждой итерации разбиваем множество на два подмножества.

Принцип разбиения:

X – произвольное множество, которое разбивается.

– подмножества, на которые разбивается множество X.

На каждой итерации свои подмножества – . Разбиение проходит по дуге. Во множество входят те гамельктоновы циклы из x, каждые из которых содержат дугу . Во множество входят те гамельктоновы циклы из x, в которых запрещена дуга , т.е. запрещен переезд в город l.

Из таких соображений выбираем дугу :

1. должно быть как можно меньше;

2. желательно выбрать , чтобы максимально возросла , следовательно, для дальнейшего разбиения выберем y.

Это приведет к возможному нахождению гамельктонова цикла, а, следовательно, к коррекции величины .

Чтобы выбрать дугу необходимо иметь матрицу , следовательно, прежде всего рассмотрим как можно получить, зная , матрицы соответствующие и .

Схема получения :

1) т. к. входит в любой гамельктоновый цикл из множества y, Поэтому вычеркиваем k – строку и l-столбец в матрице , т. к. больше не можем въезжать в город l и выезжать из города k.

 Скачать реферат