Применение производной при нахождении предела

= (1+2x++++idth=37 height=44 src="images/referats/7483/image157.png">+o (x5)) () =

1+2x+x2+x3+x4+x5+o (x5) =

1+2x+x2x3x4x5+o (x5).

Пример 4. Разложить функцию f (x) =1/cos x по формуле Тейлора с остатком Пиано по степеням x до x5 включительно. Представим функцию в виде

=1+u+u2+u3+o (u3), где u =.

Тогда

=1+u+u2+u3+o (u3) =1++++.

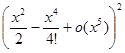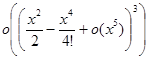При вычислении степеней

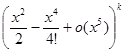
нас интересуют только слагаемые степеней не выше x5, более высокие степени войдут в o (x5). Таким образом,

=,=, =.

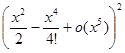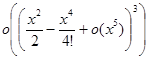Выражение

=

показывает, что в разложении

=1+u+u2+u3+o (u3)

можно, с самого начала, ограничится второй степенью

=1+u+u2+o (x5).

Подставляя нужные выражения в это равенство получим

=1+++=1+++.

Пример 5. Используя разложение из предыдущего примера, разложить функцию f (x) =tg x по формуле Тейлора с остатком Пиано по степеням x до x6 включительно.

tg x==

=

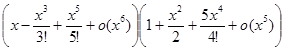x+x2 (0) +x3+x4 (0) +x5+x6 (0) =

=

Пример 6. Разложить функцию f (x) = (1+x) a - (1 - x) a по формуле Тейлора с остатком Пиано.

k = 2l+1,

Таким образом,

Следствие.

Пример 7. Используя следствие из предыдущего примера, найти предел (1401)

.

Имеем:

=|x|= sign x +o ().

Пример 8. Разложить функцию

f (x) =

по формуле Тейлора с остатком Пиано по степеням x до x4 включительно.

Сначала выпишем разложение функции по степеням x до x3 включительно.

Положим u=x - x2, тогда

==1+u+u2+u3+o (u3) =1+ x - x2+ (x - x2) 2+ (x - x2) 3+o (x3) =1+x - x3 +o (x3).

Далее,

==1+2x (1+x - x3 +o (x3)) =1+2x+2x2-2x4+o (x4).

Второй способ. Так как

,

то на первом шаге выделяем единицу:

=.

Второе слагаемое представляем в виде Cxng2 (x) так, чтобы , после чего следует представить функцию g2 (x) в виде g2 (x) = 1+g3 (x) и т.д. В нашем случае:

====

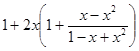==1+2x+=

 Скачать реферат