Методы решения алгебраических уравнений

Рефераты / Математика / Методы решения алгебраических уравнений

Для определения коэффициентов системы (2) удобно составить вспомогательную таблицу

В последней строке записывают сумму элементов каждого столбца, которые и являются коэффициентами системы (2).

Систему (2) обычно решают методом Гаусса.

б) y=Aecx.

Для упрощения системы (1) эту формулу, связывающую х и у, предварительно логарифмируют и заменяют формулой

1g y=1g width=85 height=21 src="images/referats/7504/image082.png">.

Система (1) примет в этом случае следующий вид:

(3)

Вспомогательная таблица имеет вид

Из систему (3) определяют с и 1g A.

в) y=Axq.

Эту формулу также предварительно логарифмируют и заменяют следующей:

Система (1) теперь примет вид

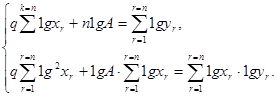(4)

Соответствующим образом изменяется и вспомогательная таблица.

2) Часто бывает необходимо заменить наилучшим образом некоторую заданную функцию у =f(x) на отрезке [a, b] многочленом m-й степени: Применение способа наименьших квадратов в этом случае приводит к отысканию коэффициентов а0, а1, …, аm из условия минимума интеграла

Необходимые условия минимума этого интеграла приводят к системе m+1 уравнений с m+1 неизвестными a0, a1, a2, ., am, из которых определяют все эти коэффициенты:

(5)

4. Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Рунге – Кутта

1. Метод Эйлера. Дифференциальное уравнение y’=f(x, y) определяет на плоскости так называемое поле направлений, т.е. в каждой точке плоскости, в которой существует функция f(x, y) задает направление интегральной кривой уравнения, проходящей через эту точку. Пусть требуется решить задачу Коши, т.е. найти решение уравнения y’=f(x, y), удовлетворяющее начальному условию y(x0)=y0. Разделим отрезок [x0, X] на n равных частей и положим (X-x0)/n=h (h – шаг изменения аргумента).Допустим, что внутри элементарного промежутка от x0 до x0+h функция y’ сохраняет постоянное значения f(x0,y0,). Тогда где y1 – значения искомой функции, соответствующее значению х1=x0+h. Отсюда получаем Повторяя эту операцию, получим последовательные значения функции:

Таким образом, можно приближенно построить интегральную кривую в виде ломаной с вершинами Mr (xr; yr), где Этот метод называется методом ломаных Эйлера, или просто методом Эйлера.

2. Метод Рунге – Кутта. Пусть функция у определяется дифференциальным уравнением y’=f(x, y) при начальном условии y(x0)=y0. При численном интегрировании такого уравнения методом Рунге – Кутта определяют четыре числа: