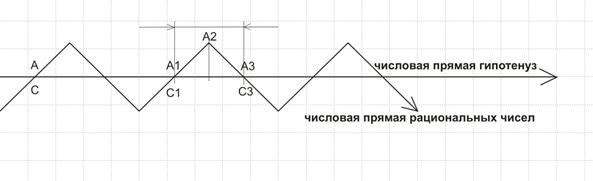
Доказательство Великой теоремы Ферма с помощью метода бесконечных (неопределенных) спусков

Метод бесконечных (неопределенных) спусков был изобретен самим П.Ферма и, очевидно, что он им пользовался для умозаключения о невозможности разложения куба на два куба, биквадрата на два биквадрата Становится совершенно очевидным факт того, что сам П. Ферма имел «чудесное» доказательство своего великого открытия.

§2. Небольшое пояснение ко второй сноске (стр. 3).

В силу закона ди

стрибутивности уравнение a2 + b2 = c2 можно преобразовать к виду к виду:

К · a2 + К · b2 = К · c2

где К – любое рациональное число

Возьмем уравнение

12 + 12 = c2

преобразуем его в вид

К12 + К12 = Кc2

2 · К = К · c2 или К · 2 = К · c2

Мы получили частное решение уравнения

если К = 2 тоc2 = К,

Уравнение c2 = К имеет решение тогда, когда есть такое рациональное число к которое образует число К по формуле:

к2 = К

отсюда следует, что если есть такое рациональное число,которое может быть образовано от числа к с помощью умножение на само себя и будет равно двум

(К = 2),то будет и решение уравнения равное этому числу (c = k) в рациональных числах.

Мы получили частное решение уравнения 12 + 12 = k2 которое, благодаря методу бесконечных (неопределенных) спусков будет источником для образования бесконечного количества решений уравнения:

12 + 12 = c2

И наоборот, уравнение 12 + 12 = c2 не будет иметь решения в рациональных числах, если отсутствует такое рациональное число, которое может быть образовано от рационального числа к с помощью умножения на само себя и будет равно двум (К = 2)

К = к 2 , а не наоборот, когда к = √ К

Если число к не определено на числовой прямой рациональных чисел, то его умножение в рациональном выражении возможно только с определенными условностями (например – округлением).

Это рассуждение, основанное на методе П.Ферма - бесконечных (неопределенных) спусков является источником объяснения того, что

12 + 12 = c2

не будет иметь решений в рациональных числах, если нет такого рационального числа, которое умноженное на само себя будет равно двум.

И будет иметь решение в действительных числах, т.к. величина к которое образует число к 2 = 2 имеет существующую зависимость от существующей величины, а значит существует.

Величина 12 + 12 - существует, существует действие умножения 1 · 1 , значит существует и величина k · k.

Т.е. про число к, которое образует число к 2 = 2 мы можем говорить лишь о том, что эта величина к существует, это действительное число, но мы да данном этапе не имеем особой меры гипотенуз (числовой оси гипотенуз), и поэтому не можем представить ее в поле мерных величин - особых рациональных числахмерного числового пространства.

© А.В. Тарасов

07. 01. 2008 г.

[1] Из разных источников

[2] Возможно, эта формула может служить источником объяснения иррациональности корня из 2, то есть невозможности решений уравнений для к = с в рациональных числах.

 Скачать реферат