Дискретно-аналоговое представление

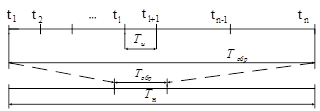
Рисунок 2

Таким образом, функция должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции , путем использования выборок в моменты времени 5 src="images/referats/8197/image025.png">.Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала , моментами времени и . Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.

Теоретически необходимо учитывать все отсчеты на интервале наблюдения , т.е. полагать = . Но при этом результаты интерполяции могут быть получены спустя время , и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией на интервале интерполяции , с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.

2. Физическая трактовка процессов интерполяции сигналов

Основное математическое соотношение интерполяционной обработки:

, (8)

можно проиллюстрировать следующим образом (рисунок 3).

В качестве интерполяционной функции в этом примере используется функция . Интервалы интерполяции и обработки должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:

. (9)

Рисунок 3

Для доказательства этого утверждения обозначим сигнал на входе и выходе линейного фильтра через и (рисунок 4):

Рисунок 4

Представим сигнал на входе линейного фильтра в виде последовательности кратковременных импульсов, площадь которых равна соответствующим выборкам

. (10)

Из свойств линейных систем следует, что сигнал на выходе равен:

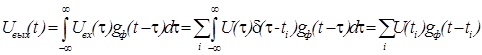(11)

Выражение (11) получается с учетом фильтрующего свойства δ-функции. Если импульсная характеристика линейного фильтра удовлетворяет выражению (9), то соотношение (11) переходит в формулу для интерполяционной обработки:

. (12)

Идеальное восстановление функции на выходе линейного фильтра невозможно, т.к.:

- отклик на выходе линейного фильтра не может появиться раньше соответствующей выборки на входе;

- число выборок не равно бесконечности;

- АЧХ фильтра отличается от идеальной.

3. Задачи идеальной интерполяции

В общем случае формула интерполяции имеет вид:

, (13)

- оценка значения i-ой выборки, - восстановленный первичный сигнал,

.

Интерполяция возможна в том случае, если в сигнале имеются корреляционные связи. Может быть поставлена задача оптимального выбора вида функции , при которой ошибка интерполяции минимальна.

Рассмотрим задачу идеальной интерполяции сигнала при предположении, что , т.е. отсутствуют внешние шумы и ошибки системы.

Пусть непрерывный первичный сигнал описывается корреляционной

функцией . Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО

. (14)

Можно показать, что в этом случае оптимальная интерполирующая функция имеет вид:

, (15)

где - весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках , .

Т.о., оптимальная интерполирующая функция может быть определена как взвешенная сумма функций времени равных корреляционной функции первичного сигнала. Как следствие этой теории может бать доказана следующая теорема:

Если на интервале интерполяции корреляционная функция и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 5).

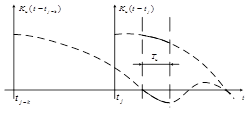
Рисунок 5

Чем меньше , тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 6):

 Скачать реферат