Лисп-реализация алгоритма кодирования информации RSA

Скорость работы алгоритма RSA

Как при шифровании и расшифровке, так и при создании и проверке подписи алгоритм RSA по существу состоит из возведения в степень, которое выполняется как ряд умножений.

В практических приложениях для открытого (public) ключа обычно выбирается относительно небольшой показатель, а зачастую группы пользователей используют один и тот же открытый (public) показа

тель, но каждый с различным модулем. (Если открытый (public) показатель неизменен, вводятся некоторые ограничения на главные делители (факторы) модуля.) При этом шифрование данных идет быстрее чем расшифровка, а проверка подписи – быстрее чем подписание.

Если k – количество битов в модуле, то в обычно используемых для RSA алгоритмах количество шагов необходимых для выполнения операции с открытым (public) ключом пропорционально второй степени k, количество шагов для операций частного (private) ключа – третьей степени k, количество шагов для операции создания ключей – четвертой степени k.

Методы «быстрого умножения» – например, методы основанные на Быстром Преобразовании Фурье (FFT – Fast Fourier Transform) – выполняются меньшим количеством шагов; тем не менее они не получили широкого распространения из-за сложности программного обеспечения, а также потому, что с типичными размерами ключей они фактически работают медленнее. Однако производительность и эффективность приложений и оборудования реализующих алгоритм RSA быстро увеличиваются.

Алгоритм RSA намного медленнее чем DES и другие алгоритмы блокового шифрования. Программная реализация DES работает быстрее по крайней мере в 100 раз и от 1,000 до 10,000 – в аппаратной реализации (в зависимости от конкретного устройства). Благдаря ведущимся разработкам, работа алгоритма RSA, вероятно, ускорится, но аналогично ускорится и работа алгоритмов блокового шифрования.

3. Функциональные модели и блок-схемы решения задачи

Функциональные модели и блок-схемы решения задачи представлены на рисунках 1 – 6.

Условные обозначения:

· P и Q – случайные простые числа;

· N – произведение простых чисел P и Q;

· PHI – значение функции Эйлера;

· E – взаимно простое число с PHI;

· PRIVATE_KEY – секретный ключ;

· LST – список простых чисел;

· NUM – число для шифрования / дешифрования;

· I, IO, I1, J, JO, R, L – рабочие переменные.

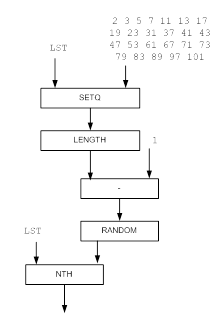
Рисунок 1 – Функциональная модель решения задачи для функции SIMPLE_NUMBER

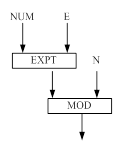
Рисунок 2 – Функциональная модель решения задачи для функции ENCRYPT

Рисунок 3 – Функциональная модель решения задачи для функции DECODING

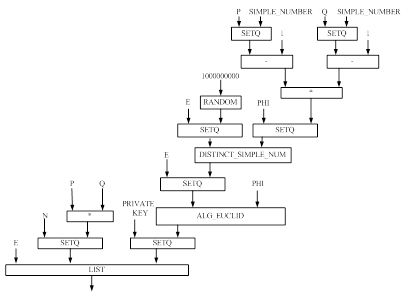
Рисунок 4 – Функциональная модель решения задачи для функции RSA

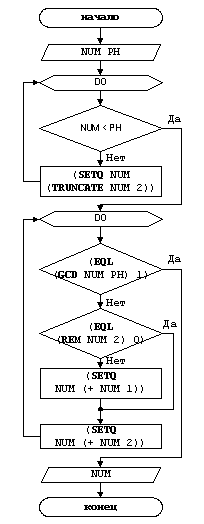
Рисунок 5 – Блок-схема решения задачи для функции DISTINCT_SIMPLE_NUM

Рисунок 6 – Блок-схема решения задачи для функции ALG_ EUCLID

4. Программная реализация решения задачи

; ПОИСК ВЗАИМНО ПРОСТОГО ЧИСЛА

(DEFUN DISTINCT_SIMPLE_NUM(NUM PH)

(DO

()

((< NUM PH) NUM)

; TRUNCATE – ЦЕЛОЧИСЛЕННОЕ ДЕЛЕНИЕ

(SETQ NUM (TRUNCATE NUM 2))

)

(DO

()

; GCD – НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ

((EQL (GCD NUM PH) 1) NUM)

; REM – ОСТАТОК ОТ ДЕЛЕНИЯ

(IF (EQL (REM NUM 2) 0) (SETQ NUM (+ NUM 1)))

(SETQ NUM (+ NUM 2))

)

)

; ГЕНЕРИРУЕМ СЛУЧАЙНОЕ ПРОСТОЕ ЧИСЛО

(DEFUN SIMPLE_NUMBER ()

; ОБЪЯВЛЕНИЕ ПЕРЕМЕННОЙ

(DECLARE (SPECIAL LST))

; СПИСОК ПРОСТЫХ ЧИСЕЛ

(SETQ LST ' (2 3 5 7 11 13 17 19 23 31 37 41 43 47 53 61 67 71 73 79 83 89 97 101))

; ВЫБИРАЕМ СЛУЧАЙНОЕ ЧИСЛО ИЗ СПСКА

(NTH (RANDOM (– (LENGTH LST) 1)) LST)

)

; РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА

(DEFUN ALG_EUCLID (X Y)

; – ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ–

(DECLARE (SPECIAL I))

(DECLARE (SPECIAL I0))

(DECLARE (SPECIAL I1))

(DECLARE (SPECIAL J0))

(DECLARE (SPECIAL J1))

(DECLARE (SPECIAL R))

(DECLARE (SPECIAL L))

;–

(IF (EQL X 1) (SETQ X (+ X Y))

; ИНАЧЕ

(PROGN

(SETQ I0 0)

(SETQ I1 1)

(SETQ L Y)

(SETQ R (REM L X))

(SETQ J0 (TRUNCATE L X))

(SETQ L X)

(SETQ X R)

(SETQ R (REM L X))

(SETQ J1 (TRUNCATE L X))

(SETQ L X)

(SETQ X R)

(DO

(())

((<= R 0) R)

(SETQ R (REM L X))

(SETQ I (– I0 (* I1 J0)))

(IF (< I 0) (SETQ I (- Y (REM (* -1 I) Y))) (SETQ I (REM I Y)))

(SETQ I0 I1)

(SETQ I1 I)

(SETQ J0 J1)

(SETQ J1 (TRUNCATE L X))

(SETQ L X)

(SETQ X R)

)

(SETQ I (– I0 (* I1 J0)))

(IF (< I 0) (SETQ I (FLOOR (- Y (REM (* -1 I) Y)))) (SETQ I (FLOOR (REM I Y))))

I

)

)

)

; РЕАЛИЗАЦИЯ АЛГОРИТМА RSA

(DEFUN RSA ()

; – ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ–

(DECLARE (SPECIAL N))

(DECLARE (SPECIAL E))

(DECLARE (SPECIAL PHI))

(DECLARE (SPECIAL PRIVATE_KEY))

(DECLARE (SPECIAL P))

(DECLARE (SPECIAL Q))

;–

; ВЫБИРАЮТСЯ ДВА ПРОСТЫХ ЧИСЛА

(SETQ P (SIMPLE_NUMBER))

(SETQ Q (SIMPLE_NUMBER))

; ВЫЧИСЛЯЕМ ИХ ПРОИЗВЕДЕНИЕ

(SETQ N (* P Q))

; НАХОДИМ PHI = (P-1) (Q-1)

(SETQ PHI (* (- P 1) (- Q 1)))

; ВЫБИРАЕМ ПРОИЗВОЛЬНОЕ ЧИСЛО

(SETQ E (RANDOM 10000000000000000))

; НАХОДИМ ВЗАИМНОЕ ПРОСТОЕ E С PHI

(SETQ E (DISTINCT_SIMPLE_NUM E PHI))

; НАХОДИМ ЗАКРЫТЫЙ КЛЮЧ PRIVATE_KEY

(SETQ PRIVATE_KEY (ALG_EUCLID E PHI))

(LIST E N PRIVATE_KEY)

)

; ПОЛУЧАЕМ КЛЮЧИ

(SETQ LIST_KEY (RSA))

(SETQ E (CAR LIST_KEY))

(SETQ N (CADR LIST_KEY))

(SETQ D (CADDR LIST_KEY))

; ШИФРОВАНИЕ ЧИСЛА

(DEFUN CODING (NUM)

(MOD (EXPT NUM E) N)

)

; ДЕШИФРОВАНИЕ ЧИСЛА

(DEFUN DECODING (NUM)

(MOD (EXPT NUM D) N)

)

; ПОЛУЧАЕМ СООБЩЕНИЕ

 Скачать реферат