Программное обеспечение системы принятия решений адаптивного робота

а модуль вектора

(2.7)

где a, b = const > 0;

dij – расстояние между активной ячейкой и МР;

c*ij – среднее значение в активной ячейке (i, j);

x0, y0– текущие координаты МР;

xi, yi – координаты активной ячейки (i, j).

Каждому из k секторов ставится в с

оответствие угол из ряда 0, a, 2a,…, 360°-a. Тогда между k и c*ij существует следующее отношение:

(2.8)

Для каждого сектора k hk вычисляется

(2.9)

Таким образом, каждая из активных ячеек находится в одном из секторов. Однако, из-за дискретности сетки, в результате такого распределения ячеек могут возникать «ступеньки» в секторах, что может привести к ошибкам в выборе направления. Для того чтобы избежать искажения результата, используется сглаживающая функция:

(2.10)

Далее вычисляется направление движения в полярных координатах, qfree, и соответствующий ему сектор kfree в H. Алгоритм выбирает более «проходимое» направление и, вместе с тем, как можно более приближенное к текущему направлению на цель qtarg.

Скорость движения МР в начальной точке устанавливается максимальной (Smax), а затем определяется на каждом шаге в соответствии с формулой:

(2.11)

где h``c = min (h`c, hm);

h`c – сглаженная полярная плотность препятствий в выбранном направлении движения;

hm – эмпирически установленная константа.

При этом отношение (*) гарантирует S` ³ 0 при h``c £ hm.

Статья [13] посвящена методу построения гладких трасс движения мобильного робота (МР), основанному на физической аналогии. Основными достоинствами метода являются устойчивое решение и работа не только с двоичными (препятствие или свободное пространство), но и с разнородными средами, поверхность которых может иметь неравные коэффициенты трения или углы наклона на различных участках.

В основе метода лежат физические принципы гидродинамики. Если предположить, что вся среда заполнена жидкостью, то потоки жидкости позволяют добраться из начальной точки в целевую. В этом случае оптимальным путем будет поток, направленный вдоль градиента давления, в котором достигается стационарное движение жидкости; локальный минимум не может быть достигнут, поскольку во всех точках потока удовлетворяется уравнение Лапласа. Для учета неоднородностей среды вводится внешняя сила, учитывающая силу трения и влияние проходимых препятствий, поэтому рассматриваются потоки вязкой жидкости. Основным уравнением движения вязкой несжимаемой жидкости является уравнение Навье-Стокса:

(2.12)

где r – плотность жидкости;

v – вектор скорости движения жидкости;

t – время;

f – внешняя сила;

p – давление;

m – коэффициент вязкости жидкости.

Упрощенное уравнение выглядит следующим образом:

(2.13)

Здесь неизвестными являются вектор скорости v и абсолютная координата x.

Граничные условия:

(2.14)

где ¶W – границы препятствий, n – внешняя нормаль к границе препятствия.

Начальные условия:

(2.15)

где xS – начальная точка, xG – целевая точка.

Для решения уравнения в двумерном пространстве методом конечных разностей уравнение представляется следующим образом:

(2.16)

где

(2.17)

Если число точек сетки N, то необходимо решить разреженную систему из 3N линейных уравнений.

Результатом работы рассматриваемого алгоритма является множество так называемых «коридоров». Каждый коридор начинается в окрестности стартовой точки и заканчивается в окрестности целевой. Следование МР по осевой линии коридора гарантирует его безопасность.

Далее рассматривается случай, когда внешняя сила не равна нулю, что позволяет учитывать разнородность среды.

Полная потенциальная энергия частицы в потоке:

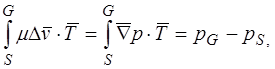(2.18)

где S – начальная точка, G – целевая точка, T – вектор, касательный к траектории, pG – pS – разность давлений в xS и xG.

В случае присутствия силы трения F:

(2.19)

Механическая работа силы трения L×F зависит от длины траектории L. В случае достаточно большой величины F:

(2.20)

Все траектории имеют ограниченную длину

(2.21)

Практически, установка очень большой величины F на границах препятствий эквивалентна условию v = 0. При использовании F = const длина потоков может быть ограничена, поэтому, увеличивая величину F, можно добиться отсеивания путей большей длины, оставляя лишь пути, длины которых близки к оптимальным.

Для тестов данного метода использовался 4-х колесный МР на полигоне 60 м ´ 100 м с препятствиями [13]. Внешняя сила f задавалась в виде:

(2.22)

где m – масса МР, q – угол наклона участка поверхности в направлении движения, Kf– коэффициент трения между колесами и поверхностью.

Следует отметить также направление, связанное с достаточно сложным по своей структуре заданием потенциальной функции, которая не имеет локальных минимумов [4, 5]. Однако при этом задание подобной потенциальной функции может оказаться очень сложным.

3. Управление мобильным роботом на основе конечно-автоматного подхода

3.1 Предпосылки создания алгоритма

Распределенные системы, в том числе робототехнические, в последнее время привлекают все большее внимание исследователей. Одна из причин этого состоит в том, что системы такого класса все чаще используются как для промышленных, так и непромышленных приложений: действительно, объединение параллельно функционирующих подсистем позволяет выполнять такие задания, которые не под силу каждой из компонент сложной системы. На рис. 3.1 приведен пример такой многокомпонентной системы, включающей мобильные роботы разного назначения: погрузчики, исследователи и т.д. С другой стороны, управление системами такого класса представляет собой нетривиальную задачу: если управление каждой из подсистем, составляющих сложную систему, задача, вообще говоря, решенная (например, перевод манипулятора из точки в точку по заданной траектории), то управление согласованным поведением группы роботов, объединенных общей целью, является сложной проблемой. Заметим, что задача управления существенно усложняется, если часть подсистем преследует конфликтующие цели.

 Скачать реферат