Устойчивость упругих систем

Очевидно, что в правой части уравнения (5) содержится пространственно-временной параметр в форме суперпозиции стоячих волн.

Учет "волны параметра" становится принципиальным, если типичная скорость продольных волн оказывается сравнимой с групповыми скоростями изгибных волн.

В противном случае можно, формально полагая, что или , ограничиться изучением следующей простейшей модели:

(6) ,

которая описывает лишь только параметрическое возбуждение системы во времени. Решение уравнения (5) можно построить с помощью метода Бубнова-Галеркина: , где - волновые числа изгибных волн; - амплитуды, определяемые из решения системы обыкновенных уравнений

(7) .

Здесь

коэффициент, содержащий параметры расстройки по волновым числам, , которые, в свою очередь, не могут быть равными нулю в отсутствие резонанса; - частоты изгибных волн при , и как и прежде - критические значения силы Эйлера.

Уравнения (7) описывают раннюю стадию эволюции волн за счет многомодовых параметрических взаимодействий. Возникает ключевой вопрос о сопоставимости возмущенных орбит системы (7) и траекторий соответствующей невозмущенной подсистемы

(8) ,

которая получается из уравнений (7) при . Другими словами, - насколько эффективен динамический отклик системы (7) на малое параметрическое возбуждение? Сначала перепишем систему (7) в эквивалентной матричной форме: , где - вектор решения; - матрица собственных чисел; - квазипериодическая матрица с компонентами на основных частотах . Следуя стандартной методике теории обыкновенных дифференциальных уравнений, решение уравнений (7) ищется в той же форме, что и для уравнений (8), где константы интеграции рассматриваются как новые искомые переменные, например , где - вектор нетривиального колебательного решения линейного однородного уравнения (8), характеризуемого набором собственных чисел . После подстановки в (7) получаются уравнения первого приближения в представлении решения рядом по малому параметру : . Правые части этих уравнений очевидно представляются суперпозицией периодических функций на комбинационных частотах . Таким образом, в первом приближении решение уравнения (7) оказывается ограниченными квазипериодическими функциями[4], когда комбинации частот ; в противном случае в системе возникают резонансы.

В нерезонансном случае можно продолжить асимптотическую процедуру нахождения решения, т.е. , для определения высших приближений к истинному решению[5]. Другими словами, мера динамического возмущения системы оказывается того же порядка, что и мера параметрического возбуждения. Напротив, в резонансном случае решение уравнений (7), вообще говоря, нельзя представить сходящимся рядом по . Следовательно, возможен эффективный отклик системы даже на очень небольшое параметрическое возбуждение. В частном случае внешнего воздействия , уравнения (7) можно весьма упростить:

(9)

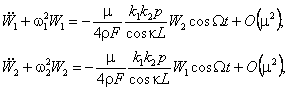
при условии, что пара изгибных волн с волновыми числами и , создает малую волновую расстройку , т.е. , и малую частотную расстройку , т.е. . Значения величин и можно также без всякого принципиального ущерба считать малыми. Выражения и можно интерпретировать как условия фазового синхронизма, необходимые для формирования резонансной тройки волн, состоящей из первичной высокочастотной продольной волны, возбуждаемой при помощи внешней гармонической силы , и вторичных низкочастотных изгибных волн, параметрически возбуждаемых за счет резонанса со стоячей продольной волной.

Заметим, что в случае упрощенной модели (6), соответствующая система амплитудных уравнений сводится к единственному уравнению типа уравнения Матье, широко применяемому во многих прикладных задачах:

Известно, что это уравнение обладает неустойчивыми решениями при малых расстойках и . Решение уравнений (7) можно найти методом Ван-дер-Поля:

(10) ; ,

где и - новые неизвестные координаты.

 Скачать реферат