Проблема когерентности световых волн

k=

разбросу частот соответствует разброс значений k. Мы установили, что временная когерентность определяется значением . Следовательно, временная когерентность связана с разбросом значений модуля волно

вого вектора к. Пространственная когерентность связана с разбросом направлений вектора к, который характеризуется величиной.

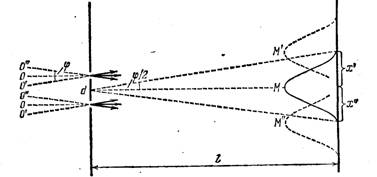
Возникновение в некоторой точке пространства колебаний, возбуждаемых волнами с разными , возможно в том случае, если эти волны испускаются разными участками протяженного (неточечного) источника света. Допустим для простоты, что источник имеет форму диска, видимого из данной точки под углом (смотри рис.4) видно, что угол характеризует интервал, в котором заключены орты . Будем считать этот угол малым. Пусть свет от источника падает на две узкие щели, за которыми находится экран (рис. 5). Интервал частот, испускаемых источником, будем считать очень малым, для того чтобы степень временной когерентности была достаточной для получения четкой интерференционной картины. Волна, пришедшая от участка поверхности, обозначенного на рис. 5 через О, создает нулевой максимум М в середине экрана. Нулевой максимум М'-, созданный волной, пришедший от участка О', будет смещен от середины экрана на расстояние х'. Вследствие малости угла и отношения d/l можно считать, что x'=/2. Нулевой максимум М", созданный волной, пришедшей от участка О", смещен от середины экрана в противоположную сторону на расстояние х", равное х'. Нулевые максимумы от остальных участков источника располагаются между максимумами М' и М".

Отдельные участки источника света возбуждают волны, фазы которых никак не связаны между собой. Поэтому интерференционная картина, возникающая на экране, будет наложением картин, создаваемых каждым из участков в отдельности. Если смещение х1' много меньше ширины интерференционной полосы x=l/d , максимумы от разных участков источника практически наложатся друг на друга и картина будет такой, как от точечного источника. При х'х максимумы от одних участков придутся на минимумы от других, и интерференционная картина наблюдаться не будет. Таким образом, интерференционная картина будет различимой при условии, что х'х, т. е.

(11)

или

(12)

При переходе от (11) к (12) мы опустили множитель 2. Формула (12) определяет угловые размеры источника, при которых наблюдается интерференция. Из этой формулы можно также определить наибольшее расстояние между щелями, при котором можно еще наблюдать интерференцию от источника с угловым размером . Умножив неравенство (12) на d/, придем к условию

(13)

Совокупность волн с разными можно заменить результирующей волной, падающей на экран со щелями. Отсутствие интерференционной картины означает, что колебания, возбуждаемые этой волной в местах нахождения первой и второй щелей, некогерентны. Следовательно, и колебания в самой волне в точках, находящихся на расстоянии d друг от друга, являются некогерентными. Если бы источник был идеально монохроматическим (это значит, что v=0 и поверхность, проходящая через щели, была бы волновой и колебания во всех точках этой поверхности происходили бы в одинаковой фазе. Мы установили, что в случае v0 и конечных размеров источника () колебания в точках поверхности, отстоящих на расстояние некогерентны.

Поверхность, которая была бы волновой при условии монохроматичности источника, будем для краткости называть псевдовол новой. Мы могли бы удовлетворить условию (12), уменьшив расстояние между щелями d, т. е. взяв более близкие точки псевдоволновой поверхности. Следовательно, колебания, возбуждаемые волной в достаточно близких точках псевдоволновой поверхности, оказываются когерентными. Такая когерентность называется пространственной. Итак, фаза колебания при переходе от одной точки псевдоволновой поверхности к другой изменяется беспорядочным образом. Введем расстояние, при смещении на которое вдоль псевдоволновой поверхности случайное изменение фазы достигает значения ~. Колебания в двух точках псевдоволновой поверхности, отстоящих друг от друга на расстояние, меньшее , будут приблизительно когерентными. Расстояние называется длиной пространственной когерентности или радиусом когерентности. Из (13) следует, что

(14)

Угловой размер Солнца составляет около 0,01 рад, длина световых волн равна примерно 0,5 мкм. Следовательно, радиус когерентности приходящих от Солнца световых волн имеет значение порядка

= 0,5/0,01 =50 мкм = 0,05 мм. (15)

Все пространство, занимаемое волной, можно разбить на части, в каждой из которых волна приблизительно сохраняет когерентность. Объем такой части пространства, называемый объемом когерентности, по порядку величины равен произведению длины временной когерентности на площадь круга радиуса . Пространственная когерентность световой волны вблизи поверхности излучающего ее нагретого тела ограничивается размером всего в несколько длин волн. По мере удаления от источника степень пространственной когерентности возрастает. Излучение лазера обладает огромной временной и пространственной когерентностью. У выходного отверстия лазера пространственная когерентность наблюдается во всем поперечном сечении светового пучка.

 Скачать реферат