Проблема когерентности световых волн

Воспользовавшись понятием времени когерентности, можно сказать, что в тех случаях, когда постоянная времени прибора много больше времени когерентности накладываемых волн), прибор не зафиксирует интерференции. Если же прибор обнаружит четкую интерференционную картину.

При промежуточных значениях четкость картины будет убывать по мере того, как растет от значений, меньших , до значений, больших .

Расстояние , на которое перемещается волна за время , называется длиной когерентности (или длиной цуга). Длина когерентности есть то расстояние, на котором случайное изменение фазы достигает значения ~п. Для получения интерференционной картины путем деления естественной волны на две части необходимо, чтобы оптическая разность хода была меньше, чем длина когерентности. Это требование ограничивает число видимых интерференционных полос, наблюдаемых по схеме на рис 1.

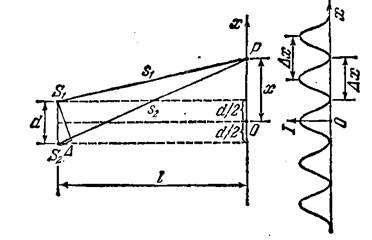
С увеличением номера полосы m разность хода растет, вследствие чего чекость полос делается все хуже и хуже. Перейдем к выяснению роли немонохроматичности световых волн. Допустим, что свет состоит из последовательности идентичных цугов частоты и длительности . При смене одного цуга другим фаза претерпевает беспорядочные изменения, вследствие чего цуги оказываются взаимно некогерентными. При этих предположениях дли-тельность цуга практически совпадает со временем когерентности .

В математике доказывается теорема Фурье, согласно которой любую конечную и интегрируемую функцию F (t) можно представить в виде суммы бесконечного числа гармонических составляющих с непрерывно изменяющейся частотой

(4)

Выражение (4) называется интегралом Фурье. Стоящая под знаком интеграла функция А () представляет собой амплитуду соответствующей монохроматической составляющей. Согласно теории интегралов Фурье аналитический вид функции А () определяется выражением

А () = (5)

где — вспомогательная переменная интегрирования. Пусть функция F(t) описывает световое возмущение в некоторой точке в момент времени t, вызванное одиночным волновым цугом.

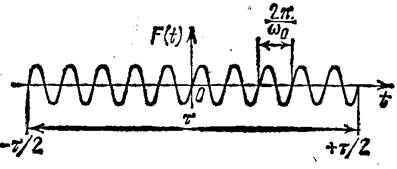
Тогда она определяется условиями:

F(t)=при

F(t)=0 при

График вещественной части этой функции дан на рис.2. Вне интервала от-до +функция F (t) равна нулю. Поэтому выражение (5), определяющее амплитуды гармонических составляющих, имеет вид

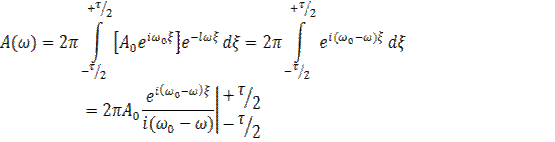
После подстановки пределов интегрирования и несложных преобразований приходим к формуле

Интенсивность I() гармонической составляющей волны пропорциональна квадрату амплитуды, т. е. выражению

(6)

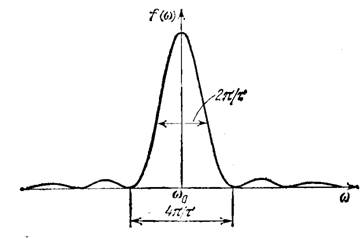
График функции (6) показан на рис. 3. Из рисунка видно, что интенсивность составляющих, частоты которых заключены в интервале

значительно превосходит интенсивность остальных составляющих. Это обстоятельство позволяет связать длительность цуга с эффективным частотным диапазоном фурье-спектра:

Отождествив со временем когерентности, придем к соотношению:

(7)

Из соотношения(7) следует, что чем шире интервал частот, представленных в данной световой волне, тем меньше время когерентности этой волны. Частота связана с длиной волны в вакууме соотношением . Продифференцировав это соотношение, найдем, что

(знак минус, получающийся при дифференцировании, мы опустили, кроме того, положили ). Заменив в формуле(7) его выражением через и , получим для времени когерентности выражение

(8)

Отсюда для длины когерентности получается следующее значение:

(9)

Разность хода, при которой получается максимум m-го порядка, определяется соотношением:

Когда эта разность хода достигает значения порядка длины когерентности, полосы становятся неразличимыми. Следовательно, предельный наблюдаемый порядок интерференции определяется условием:

откуда

(10)

Из (10) следует, что число интерференционных полос, наблюдаемых по схеме, изображенной на рис.1, возрастает при уменьшении интервала длин волн, представленных в используемом свете. Пространственная когерентность. Согласно формуле

 Скачать реферат