Туннельный эффект (холодная эмиссия электронов и контактная разность потенциалов)

Таким образом, в рамках классической теории невозможно объяснить с количественной стороны явление холодной эмиссии.

В квантовой теории, когда допустимо прохождение электронов сквозь потенциальный барьер, для потенциальной энергии можно ограничиться выражением (3.9) и не учитывать сил электрического изображения, поскольку последние лишь весьма незначительно изменят окончательный результат. И

з графика потенциальной энергии (рис 3.2) видно, что внешнее электрическое поле создает потенциальный барьер конечной ширины. Благодаря туннельному эффекту электрон может преодолеть этот барьер, причем коэффициент прозрачности равен

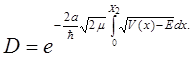(3.16)

Интеграл в экспоненте должен быть взят по всей ширине барьера от точки х=0 до точки х=х1, которая определяется из условия

(3.17)

Тогда

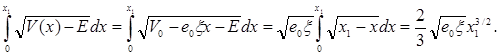(3.18)

Окончательно для коэффициента прозрачности D получаем выражение:

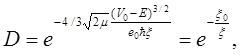(3.19)

где величина ξ0 зависит от работы выхода из металла свободных электронов. Ток холодной эмиссии пропорционален коэффициенту прозрачности

(3.20)

Отсюда следует, что холодная эмиссия должна наблюдаться при напряженности электрического поля ξ~106 в/см, что хорошо согласуется с экспериментальными данными.

§ 4. Контактная разность потенциалов

На основе туннельного эффекта можно объяснить и явление так называемой контактной разности потенциалов, которое было открыто ещё Вольтом.

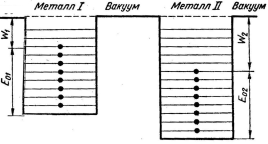
рис 4.1 Два металла до сближения: W1 и W2 – работа выхода; E01 b E02 – верхние границы заполненных уровней (энергия Ферми)

Рассмотрим два металла различной природы, обладающих различными работами выхода, а вместе с тем и уровнями Ферми (рис 4.1). Если привести их в соприкосновение, то они оказываются разделенными потенциальным барьером конечной ширины. Поскольку часть занятых электронами энергетических уровней в металле I лежит выше границы заполненных уровней металла II, возможен туннельный переход электронов на свободные уровни металлов II. Обратный переход, как видно из 6.6, исключен, поскольку электроны металла II при таком переходе будут иметь энергию, соответствующую заполненным уровням металла I. Очевидно, далее, что возникший электрический ток прекратится только в том случае, когда верхнее заполненные уровни металлов сравняются.

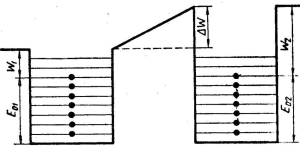
рис 4.2 Два металла после сближения. Возникновение контактной разности потенциалов.

В результате туннельного эффекта металл II, получив избыток электронов, заряжается отрицательно и соответственно металл I заряжается положительно. При этом начало отсчета энергетических уровней металла II поднимается вверх по отношению к началу отсчета уровней металла I (рис 4.2). После того как наступило термодинамическое равновесие, при котором уровни Ферми в обоих металлах должны сравняться, электрический ток прекратится, но зато между металлами возникает разность потенциалов, пропорциональная разности работ выхода:

(4.1)

Эта величина и представляет собой контактную разность потенциалов.

Заключение

Туннельный эффект обусловливает возможность протекания термоядерных реакций на Солнце и звёздах при температуре в десятки и сотни млн. градусов, а также в земных условиях в виде термоядерных взрывов.

В симметричном потенциале, состоящем из двух одинаковых ям, разделённых слабопроницаемым барьером, туннельный эффект приводит к интерференции состояний в ямах, что приводит к слабому двойному расщеплению дискретных уровней энергии. Для бесконечного периодичного в пространстве набора ям каждый уровень превращается в зону энергий. Таков механизм образования узких электронных энергетических зон в кристаллах с сильной связью электронов с узлами решётки.

Если к полупроводниковому кристаллу приложено электрическое поле, то зоны разрешённых энергий электронов становятся наклонными в пространстве. Тем самым уровень потенциальной энергии электрона пересекает все зоны. В этих условиях становится возможным переход электрона из одной энергетической зоны в другую за счёт туннельного эффекта. Классически недоступной областью при этом является зона запрещённых энергий. Это явление называется пробоем Зинера. Квазиклассическое приближение отвечает здесь малой величине напряжённости электрического поля. В этом пределе вероятность пробоя Зинера определяется в основном экспонентой, в показателе которой стоит большая отрицательная величина, пропорциональная отношению ширины запрещённой энергетической зоны к энергии, набираемой электроном в приложенном поле на расстоянии, равном размеру элементарной ячейки.

Похожий эффект проявляется в туннельных диодах, в которых зоны наклонены благодаря полупроводникам р- и n-типа по обе стороны от границы их соприкосновения. Туннелирование осуществляется благодаря тому, что в зоне, куда переходит носитель заряда, имеется конечная плотность незанятых состояний.

Благодаря туннельному эффекту возможен электрический ток между двумя металлами, разделёнными тонкой диэлектрической перегородкой. Эти металлы могут находиться как в нормальном, так и в сверхпроводящем состоянии. В последнем случае может иметь место Джозефсона эффект.

Туннельному эффекту обязаны такие явления, происходящие в сильных электрических полях, как автоионизация атомов и автоэлектронная эмиссия из металлов. В обоих случаях электрическое поле образует барьер конечной прозрачности. Чем сильнее электрическое поле, тем прозрачнее барьер и тем сильнее электронный ток из металла. На этом принципе основан сканирующий туннельный микроскоп - прибор, измеряющий туннельный ток из разных точек исследуемой поверхности и дающий информацию о характере её неоднородности. Используя туннельный ток как индикатор приближения к поверхности и нарисовав несколько вариантов её профилей, можно сложить из рисунков трехмерную картинку исследуемой поверхности. Сканирующий микроскоп, удерживая постоянную величину туннельного тока, рисует ту поверхность, на которой вероятность пребывания электронов постоянна, то есть, по сути, ту самую пси-функцию, которую используют для описания квантовых объектов.

Туннельный эффект возможен не только в квантовых системах, состоящих из одной частицы. Так, например, низкотемпературное движение дислокаций в кристаллах может быть связано с туннелированием конечной части дислокации, состоя из многих частиц. В такого рода задачах линейную дислокацию можно представить как упругую струну, лежащую первоначально вдоль оси у в одном из локальных минимумов потенциала V(x, у). Этот потенциал не зависит от у, а его рельеф вдоль оси х представляет собой последовательность локальных минимумов, каждый из которых находится ниже другого на величину, зависящую от приложенного к кристаллу механического напряжения. Движение дислокации под действием этого напряжения сводится к туннелированию в соседний минимум определенного отрезка дислокации с последующим подтягиванием туда оставшейся её части. Такого же рода туннельный механизм может отвечать за движение волн зарядовой плотности в диэлектрике Пайерлса.

 Скачать реферат